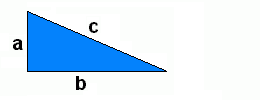
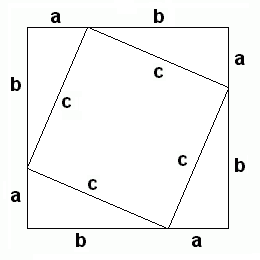
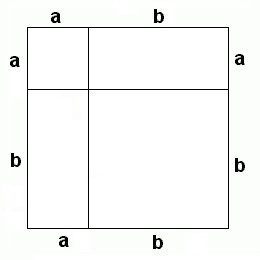
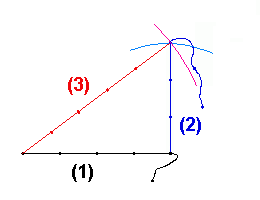
Note on the Pythagorean Theorem

The Pythagorean Theorem can in fact be traced back to a Babylonian clay tablet dated ca. 1800 B.C. And whether Pythagoras (ca. 560 - ca. 480 B.C.) or one of his scholars was the first to elaborate its proof can't be claimed with any degree of credibility. Nevertheless, the geometric identity describing the relation between the length of the three sides of a right triangle is known as the Pythagorean Theorem:

  a² + b² = c²

Where a and b are the lengths of the orthogonal sides and c is the length of the hypotenuse or "oblique" side of the triangle.

Euclid's "Elements" (ca. 300 B.C.) was the first - and for many centuries remained the only - standard reference in Geometry. In this work Euclid supplied two very different proofs for the Pythagorean Theorem. Euclid also mentioned and proofed that the Theorem is reversible, which means that a triangle whose sides satisfy a² + b² = c² is necessarily right angled. The theorem of Pythagoras is of fundamental importance in the Euclidean Geometry where it serves as a basis for the definition of distance between two points in an orthogonal grid.

Mathematical Philosophy

The earliest recorded beginnings of geometry can be traced to ancient Egypt the ancient Indus Valley, and ancient Babylonia from around 3000 BC. Early geometry was a collection of empirically discovered principles concerning lengths, angles, areas, and volumes, which were developed to meet some practical need in surveying, construction, astronomy, and various crafts. Among these were some surprisingly sophisticated principles, for example, both the Egyptians and the Babylonians were aware of versions of the Pythagorean theorem about 1500 years before Pythagoras.

Pythagoras and his scholares considered Numbers to be the true nature of things and they established a religious philosophy in which mathematics played an important role. It was the Pythagoreans who discovered that the relationship between musical notes could be expressed in numerical ratios of small whole numbers. In fact they started to treat the "theory of numbers" as a new dicipline in mathematics. In elementary number theory, integers are studied without use of techniques from other mathematical fields. Questions of divisibility, greatest common divisors, factorization of integers into prime numbers, investigation of perfect numbers and congruences belong here.

On the other hand the Pythagoreans realized that numbers and geometry (the study of shapes) were closely related and that geometric problems could be solved with cognition of number theory but also that questions in number theory could be geometricaly solved.
These "bridges" between different mathematical diciplines is a very strong instrument to solve a difficult problem in one dicipline by translating it into another dicipline in with a solution can be elaborated more easily and then translating the solution back to the original dicipline.
The bridge between numbers and geometry is the fact that sides, area or volume of physical shapes can be related to a number. The basis for this is the term "length". The length of some physical distance is defined as the number of times a (physical) reference distance (e.g. one Meter) is included in the unknown distance. The result is a number and a unit (the unit being the reference length used to obtain the number).

Proof of the Phytagorean Theorem

A simple (geometrical) proof of the Phytagorean theorem can be elaborated as described below. It is based on the following two "presumptions":

the area of a rectangle with the side lengths x and y is Ar = x*y
The area of a right triangle with orthogonal side lengths x and y is: At = x*y/2

The basic right triangle is shown on the right. The length of the ortogonal sides is a and b. The length of the hypotenuse is c. The unit of length for a, b and c is a linear scaling factor and is not significant for the Pythagorean Theorem, which deals with a "relative" relationship between sides. The only requirement is that when dealing with "numbers" for the sides, the unit of length must be the same for a,b and c.
Now study the geometric arrangement on the right, which is composed of four identical triangles arranged such that they form a big square: The area of the outer square can be calculated in two ways: by calculating the area from the length of the sides: A1 = (a+b)(a+b) = (a+b)² by summing up the areas of the inner square and the four right triangles: A2 = cc + 4(ab/2) = c² + 2(ab) The areas A1 and A2 must be identical since they are related to the same form. This yields: (a+b)² = c² + 2(ab) (1)
The algebraic equivalent for (a+b)² can be elaborated from the following (geometric) arrangement: The area (a+b)² can be divided in the sum of the areas of the squares and the areas of the two rectangles: (a+b)² = a² + b² + 2(ab) (2) This is valid for any pair of numbers a and b and is a general algebraic identity. Replacing (a+b)² in (1) by it's algebraic equivalent according to (2) yields: a² + b² + 2(ab) = c² + 2(ab) a² + b² = c² This is valid for the relationship between the sides of any right triangle.
Euclid also showed, that when the sides of triangle fullfill the Pythagorean Identity, the triangle has orthogonal sides. Moreover, a triple of whole numbers (a,b,c), which fullfill the Pythagorean Identity, is called a Pythagorean Triple. A well known Pythagorean Triple is (3,4,5). Another such triple is (5,12,13). It is clear, that if (a,b,c) is a Pythagorean Triple and "k" is a scalar, then also (ka,kb,k*c) is a Pythagorean Triple.
A practical application of the reversability of the Pythagorean Theorem and Pythagorean Triples could have been the construction of rectangular floor plan e.g. for a greek temple. All you need for this is a cord with 3 knots marking 3 different lengths, which must be derived from a Pythagorean Triple. E.g. The knots could be at 15, 20 and 25 passus (ancient greek unit of length; 1 passus = 1.542 m). The tripple (15,20,25) is derived from 5*(3,4,5). The necessary steps for the floor plan construction are shown on the right. The cord used has a length of 25 passus with knots each 5 passus apart. First one side of the building - 20 passus long - may be aligned to some object in it's vincinity (1). This already marks two of the four vertix points of the building to be raised. After this the short side - 15 passus long - is marked on the sand as a circle (2). From the other point of the long side, the 25 passus long hypothenuse is drawn as a circle in the sand (3). The point where both circles marking the 25 passus distance and the 15 passus distance intersect, is the third vertex point of the building yielding two orthogonal sides. Similarly, the last vertex point can be constructed giving an exact rectangular floorplan for the building.

Cover << Sail Away << Notes on Trigonometry << Notes on Plane Trigonometry << .

last updated: 28-Apr-2006