Notes on Plane Trigonometry
Plane trigonometry deals with the relations between the angles and sides of triangles
of which the three vertices are located on the surface of a plane and the sides are straight
lines (a straight line being the shortest connection between two points on the plane). Types of Angles
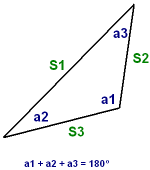
The Plane Oblique Triangle
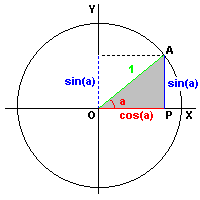
Basic Trigonometric Functions
Fundamental IdentitiesThe following general identities can be easily verified by drawing the right triangles corresponding to the angles involved.sin2(x) + cos2(x) = 1 sin(-x) = -sin(x) cos(-x) = cos(x) sin(x) = sqrt(1-cos2(x)) cos(x) = sqrt(1-sin2(x)) sin(a+90°) = cos(a) sin(a-90°) = -cos(a) cos(a+90°) = -sin(a) cos(a-90°) = sin(a) sin(90°-a) = cos(a) cos(90°-a) = sin(a) tan(a) = sin(a)/cos(a) ctan(a) = 1/tan(a) = cos(a)/sin(a) Special EquationsSum of anglessin(a+b) = sin(a)*cos(b) + cos(a)*sin(b) sin(a-b) = sin(a)*cos(b) - cos(a)*sin(b) cos(a+b) = cos(a)*cos(b) - sin(a)*sin(b) cos(a-b) = cos(a)*cos(b) + sin(a)*sin(b) tan(a+b) = [tan(a)+tan(b)]/[1-tan(a)*tan(b)] Sum of sine and cosinesin(a) + sin(b) = 2 * sin((a+b)/2) * cos((a-b)/2) sin(a) - sin(b) = 2 * cos((a+b)/2) * sin((a-b)/2) cos(a) + cos(b) = 2 * cos((a+b)/2) * cos((a-b)/2) cos(a) - cos(b) = -2 * sin((a+b)/2) * sin((a-b)/2) Product of sine and cosinesin(a) * cos(b) = [sin(a+b) + sin(a-b)]/2 cos(a) * cos(b) = [cos(a+b) + cos(a-b)]/2 sin(a) * sin(b) = [cos(a-b) - cos(a+b)]/2 Half-anglesin(a/2) = ±sqrt( (1-cos(a)) / 2 )
cos(a/2) = ±sqrt( (1+cos(a)) / 2 )
tan(a/2) = ±sqrt( (1-cos(a)) / (1+cos(a)) )
= sin(a) / (1+cos(a))
= (1-cos(a)) / sin(a)
In the equations above, the correct sign of the sqrt() result must be chosen from the specific configuration.Reverse Identitiesasin(-x) = -asin(x) acos(-x) = acos(x) acos(x) + acos(-x) = 180° (π) asin(x) + acos(x) = 90° (π/2) |
Graphical Interpretation of Trigonometric Relations
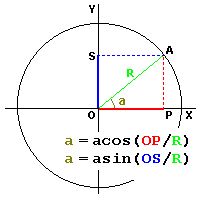
The reverse functions "acos(x)" and "asin(x)"
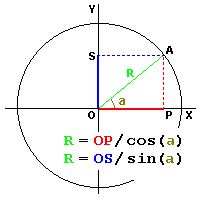
The inverse functions "1/cos(x)" and "1/sin(x)"
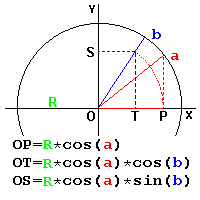
The products of "cos(x)" and "sin(x)" values
| Cover << Sail Away << Notes on Trigonometry << . | . >> Spherical Trigonometry | last updated: 07-Jan-2011 |