Position at 15:39 UTC on June 03. 2011
Here is an example using only one celestial object - the Sun - with a couple of
hours of time difference between two fixes.
This will require "advancing" the first Line-of-Position over the distance sailed during the
time between the two fixes.
Our position was about 50 miles NW of Cape Finisterre (North Spain).
To check the accuracy of the celestial procedure, the GPS position was recorded
for both fixes:
UTC 11:32:15 UTC 15:38:39
N 43° 52'5 N 43° 25'5
W 010° 03'5 W 010° 08'5
The weather was clear for both sights, the sea was moderate with moderate swell
and wind 4 to 5 Bft from NW.
The measurements were obtained under the following conditions:
The chronometer was synchronized to UTC time
with the GPS receiver and there was no chronometer error for both sights. The index error (IE) was checked before and after
the altitude measurements and was +0'8 minutes of arc in both cases. During the measurements I was standing in the cockpit,
with the sextant about 3.5 meters above the sea level.
This implies a dip error of -3.3 minutes of arc (from the
"Correction Table for Dip"). Since the measurements were taken over a time
span of several hours, the dispacement of the vessel must be taken into
account by "advancing" the first Line-of-Position over the sailed distance
and course (27 Nm in 188°).
The measured altitudes were:
object chronometer altitude limb
Sun : 11:32:15 64° 14'2 lower
Sun : 15:38:39 47° 10'7 lower
From the Nautical Almanac 2011 the
June-03rd page
will be needed.
Time of Observation
First the correct times of observation are recorded in the
Altitude Worksheet:
| Sun 1132 | | Sun 1539 |
|---|
Section 1 "Time of Observation"
Date 03 June 2011
Chronometer 11 h 32 m 15 s
Error + 00 m 00 s
__________________
Local Time ____h ___m ___s
Time Zone ± ____h
__________________
UTo 11 h 32 m 15 s
Object _ SUN __ upper
limb
|
needed only if
< chronometer set >
to local time
|
Section 1 "Time of Observation"
Date 03 June 2011
Chronometer 15 h 38 m 39 s
Error + 00 m 00 s
__________________
Local Time ____h ___m ___s
Time Zone ± ____h
__________________
UTo 15 h 38 m 39 s
Object _ SUN __ lower
limb
|
Since our chronometer is already set to UTC, local time and time-zone correction
are not used here. The results are the times of observation (UTo) in the
Universal Time system.
Observed Altitude
In this section the corrections on the measured sextant angles (Hs) are applied
(Section 2 of the Altitude Worksheet).
Beside the sextant altitude, the name of the sighted object and the approximate compass
direction are recorded. The value of the compass direction can be used to check the
calculated azimuth.
The index error was 0.0 minutes of arc and the dip correction is -2.2 minutes
of arc corresponding to an observation height of 1.5 meters above the sea
level.
For the refraction correction, the entries for 1030hPa / 30°C are used
(from the
"Correction Table for Refraction").
| Sun 1132 | | Sun 1539 |
|---|
Section 2 "Altitude"
Hs 64° 14'2 cel.obj. Sun
IE + 0'8 app.dir. 140°
Dip - 3'3
________________
Ha 64° 11'7
SD + 15'8 lower limb: +
upper limb: -
Refr - 0'4
________________
64° 27'1
Prllx + 0° 00'0 HP 0° 00'1
________________
Ho 64° 27'1
|
Dip, Refr and Prllx
are found in the
Correction Tables
for
Sextant Altitudes
SD and HP are in the
Nautical Almanac
|
Section 2 "Altitude"
Hs 47° 10'7 sel.obj. Sun
IE + 0'8 app.dir. 250°
Dip - 3'3
________________
Ha 47° 08'2
SD + 15'8 lower limb: +
upper limb: -
Refr - 0'9
________________
47° 23'1
Prllx + 0° 00'1 HP 0° 0'1
________________
Ho 47° 23'2
|
The next step is to find the geographical coordinates of
the sighted celestial objects at the time of observation. These coordinates
are required to further calculate the Altitude and Azimuth of these objects
at the estimated position.
Finally, the calculated Altitude (Hc) must be compared to the measured
Altitude (Ho) and the appropriated Line-of-Position can then be constructed.
Geographical Position of the Celestial Objects
in Section 3 "Nautical Almanac" of the
Altitude Worksheet
the Geographical Positions of the observed objects have to be elaborated.
For working out this section the
June-03rd page
from the 2011 Nautical Almanac is required. From this page the GHA and Dec values
for 11:00 UTC and 15:00 are extracted as well as the increment values ddGHA and dDec
in the same lines.
The procedure for the GHA looks like this:
| Sun 1132 | | Sun 1539 |
|---|
Section 3 "Nautical Almanac (GHA)"
GHA(NA) 345° 28'4 ddGHA -00'1
dHA +___° __'_ 15°/h
Interp ± __'_
________________
GHA ___° __'_ at time of obs.
|
-- June 03rd --
|
Section 3 "Nautical Almanac (GHA)"
GHA(NA) 045° 28'0 ddGHA -00'1
dHA +___° __'_ 15°/h
Interp ± __'_
________________
GHA ___° __'_ at time of obs.
|
For the GHA there are two interpolated values. The first value (dHA) is the
fraction of the hour after 12:00 UTC associated with a constant increase
of the GHA of 15°/h.
This value is found in the dHA columns of the
Interpolation Tables for Celestial Navigation.
For the Noon Sight look into the 32Min/15Sec entry
and for the Afternoon Sight look for the 38Min/39Sec entry.
This yields the values
08° 03'8 for the first and 09° 39'7 for the second Sight.
The sign of these first interpolation values is always positive.
The second interpolated value is related to the additional increase
or decrease of the GHA (additional to the fixed 15°/h). To evaluate this,
the second (right) part of the "Nautical Almanac" section in the
Altitude Worksheet
is used:
| Sun 1132 | | Sun 1539 |
|---|
Section 3 "Nautical Almanac (GHA)"
Interpolation of Greenwich Hour Angle (GHA) |
Interp. Tab. |
Section 3 "Nautical Almanac (GHA)"
Interpolation of Greenwich Hour Angle (GHA) |
ddGHA 00'1 --> log(d) 07781
f 32' 15" --> log(f) 32866
+ _______
c=d*f/60 00'1 <-- 40647
|
column "p"
column "p"
column "s"
|
ddGHA 00'1 --> log(d) 07781
f 27' 49" --> log(f) 33653
+ _______
c=d*f/60 00'1 <-- 41434
|
Notice that this interpolation scheme does not take into account the correct sign
of the interpolated value (increment or decrement).
This sign of the result must be obtained from the ddGHA value of the Nautical Almanac.
The interpolation results (-00.1 minutes of
arc for both measurements) are then used together
with the looked-up interpolation results for the 15°/h GHA increase,
to obtain the correct GHA values for the two fixes:
| Sun 1132 | | Sun 1539 |
|---|
Section 3 "Nautical Almanac (GHA)"
GHA(NA) 345° 28'4 ddGHA -00'1
|
Interp +008° 03'8 15°/h |
|
Interp - 00'1 <---
________________
GHA 353° 32'1 at 11:32:15 UTC
|
-- June 03rd --
|
Section 3 "Nautical Almanac (GHA)"
GHA(NA) 045° 28'0 ddGHA -00'1
|
Interp +009° 39'7 15°/h |
|
Interp - 00'1 <---
________________
GHA 055° 07'6 at 15:38:39 UTC
|
The elaboration of the correct Declination values is similar to the GHA
procedure. The values for Dec and dDec from the Nautical Almanac are transferred
to the Worksheet and the dDec values are interpolated the same way as the
ddGHA values were interpolated. The result is the Declination of each Sight
for the exact time of observation:
| Sun 1132 | | Sun 1539 |
|---|
Section 3 "Nautical Almanac (Dec)"
Dec N 22° 17'9 dDec +00'3
|
Interp + 00'2 <---
______________
Dec N 22° 18'1 at 11:32:15 UTC
|
-- June 03rd --
|
Section 3 "Nautical Almanac (Dec)"
Dec N 22° 19'1 dDec +00'4
|
Interp + 00'2 <---
______________
Dec N 22° 19'3 at 15:38:39
|
The interpolation scheme for the Declination is shown in the following table.
Notice that the conversion for the hour fractions (32' 15" and
38' 39") have already been looked up while interpolating
the ddGHA values and can be reused:
| Sun 1132 | | Sun 1539 |
|---|
Section 3 "Nautical Almanac (Dec)"
Interpolation of Declination (Dec) |
Interp. Tab. |
Section 3 "Nautical Almanac (Dec)"
Interpolation of Declination (Dec) |
dDec 00'3 --> log(d) 12552
f 32' 15" --> log(f) 32866
+ _______
c=d*f/60 04'8 <-- 45418
|
column "p"
column "p"
column "s"
|
ddGHA 00'4 --> log(d) 13802
f 38' 39" --> log(f) 33653
+ _______
c=d*f/60 00'2 <-- 47455
|
It is always good practice to double-check the interpolated results by doing
some simple inspections. The hour fraction can be rounded to the next quarter
of an hour and then the result of the interpolation should be close to 1/4th,
2/4th, 3/4th or 4/4th of the ddGHA/dDec value. In this example the hour fraction
is between half and 3/4 of an hour for both sights.
So, the interpolated values must be slightly higher than half the ddGHA/dDec
values:
ddGHA ddGHA dDec dDec
full-hour -00'1 -00'1 -00'3 +00'4
interpolated -00'1 -00'1 -00'2 +00'2
Now, the Geographical Positions of the sighted objects
at the time of obervation is exactly known, and both the Altitude and the
Azimuth can be calculated for the locations of the Estimated Position.
This process is called "Sight Reduction".
Sight Reduction
For the process of Sight-Reduction there are basically three alternative
methods:
- Use Tables of Altitude/Azimuth for pre-defined locations
(Worksheet available)
- The method of Ageton using logarithmic sine/cosine tables
(Worksheet available)
- Use an electronic calculator or special software applications
The electronic method can also consist of a web-based application such as
the
interactive Nautical Calculator.
This form will calculate the observers position from the known data:
Estimated Position, the Geographical Position of two sighted object and the
measured Altitudes.
The result from this application is ( N 43° 25.2' W 010° 06.0).
This position is about 2 nautical miles away from the GPS position.
This difference, which demonstrates the order of accuracy obtainable with
celestial navigation techniques, is principally due to measurement errors.
These inherent inaccuracies can be reduced by averaging a couple of measurements,
which is rather sumptuous, but also by practice! With some experience it
should be possible to make celestial fixes with an accuracy better that 2
nautical miles provided good measurement conditions (smooth sea, good visibility,
mid-range altitude, ...).
Without Nautical Calculator, the process of finding the position from the
observed altitude and Geographical Position (sight reduction) can
be performed with the precompiled Sight Reduction Tables.
The compiled Sight Reduction Tables
produce the Altitude and Azimuth Angle for integral degrees of Assumed
Position of the observer and Geographical Position of the sighted object
(select the appropriate table from the
Manual Download Section).
By choosing the appropriate Assumed position, both the Local Hour Angle
and the Latitude will be integer values.
The exact value of the Declination must be taken into account by
interpolating between two altitude values from the Sight Reduction Tables.
The procedure is as follows:
Choose an Assumed Position as close as possible
to the Estimated Position, such that both the Local Hour Angle as well
as the Assumed Latitude are integral degree values.
This has to be done separately for each observation. Use these new Assumed Positions as reference points
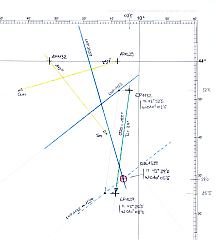
for the graphical evaluation of position on the plotting sheet. - Determine the calculated Altitudes and Azimuth Angles for both observations.
- Plot the Lines-of-Position in an appropriate plotting sheet.
In the above example, the Estimated Position and the Geographical Positions were:
Position 1 GP (sun) Position 2 GP (sun)
N 43° 52'5 N 22° 18'1 N 43° 25'5 N 22° 19'3
W 010° 03'5 353° 32'1 W 010° 08'5 055° 07'6
The corresponding Assumed Positions and input arguments for the Sight Reduction
Tables (shown in red) are (note that for the Assumed Position both Latitude and Longitude are changed):
Assumed Assumed
Position 1 GP (sun) LHA=GHA+Lon Position 2 GP (sun) LHA=GHA+Lon
N 44° 00'0 N 22° 18'1 N 44° 00'0 N 22° 19'3
W 010° 32'1 353° 32'1 343° 00'0 W 010° 07'6 055° 07'6 045° 00'0
With the above numbers marked in red and the correct part of the
Sight-Reduction manual
(Declination SAME as Latitude), the worksheet for this will be as follows.
For the first sight, the enties are: Lat=44°, Dec=22° and LHA=343°
Section 4 "Sight Reduction"
GHA 353° 32'1
E:+ W:-
LonAP - 010° 32'1 LatAP N 44° --> go to volume "40° - 49°"
________________ of the Sight Reduction Tables
Dec - Lat
LHA 343° Dec N 22° 18'1 SAME / CONTRARY
with Declination same as Latitude
N-Lat LHA>180°: Zc=Z
H 63° 54'1 dH +52'4 Ref 0° LHA<180°: Zc=360°-Z
S-Lat LHA>180°: Zc=180°-Z
Interp + 15'8 Z + 142° LHA<180°: Zc=180°+Z
________________ ________________
Hc 64° 09'9 Zc 142°
Ho - 64° 27'1
________________
Hd -17'2
|
And the worksheet for the second sight with the following entries for the Sight-Reduction
tables: Lat=44°, Dec=22° and LHA=045°
Section 4 "Sight Reduction"
GHA 055° 07'6
E:+ W:-
LonAP - 010° 07'6 LatAP N 44° --> go to volume "40° - 49°"
________________ of the Sight Reduction Tables
Dec - Lat
LHA 045° Dec N 22° 19'3 SAME / CONTRARY
with Declination same as Latitude
N-Lat LHA>180°: Zc=Z
H 47° 02'4 dH +39'6 Ref 360° LHA<180°: Zc=360°-Z
S-Lat LHA>180°: Zc=180°-Z
Interp + 12'7 Z - 105°8 LHA<180°: Zc=180°+Z
________________ ________________
Hc 47° 15'1 Zc 254°2
Ho - 47° 23'2
________________
Hd -7'1
|
The values for H obtained from the Sight-Reduction Tables, must be improved by
interpolating dH for the correct Declination.
This is done similar to the interpolation of the Nautical Almanac data with the
Interpolation Tables for Celestial Navigation.
Line-of-Position
|
In the final section of the
Altitude Worksheet the data required to construct the Line-of-Positon is
assembled.
The obtained results from the Sight-Reduction procedure above,
(Hd=-17'2 / Zc=142° for the first and Hd=-7'1 / Zc=254° for the second fix as well
as the Assumed Positions for both results) can be used to draw two Lines-of-Position.
In this way a position from two celestial observations can be
elaborated graphicaly,
similar to the intersection of two bearing lines as used in terrestrial navigation.
For plotting the Lines-of-Position, a plotting sheet with a Mercator grid is required.
This is simply a blank nautical chart with a latitude-dependend ratio of the latitude-
to the longitude scale and can be constructed graphically or directly printed from
the appropriate page from the available
Mercator Plotting Sheets.
|
 |
| 