Celestial Navigation

Celestial Navigation is a very elaborate system. It took literally centuries and generations of navigators, astronomers, mathematicians and instrument makers to develop, not reaching its present form until 1877. In the early ages of maritime navigation long before the magnetic compass emerged, the Sun and some selected stars were used as an aid for orientation to check and correct courses. Viking navigators explored the northern Atlantic region between Norway and Canada navigating mainly by the Sun at daytime and by some circumpolar stars at night.

Later, as more precise ephemeral data became available and improved optical measurement instruments had been developed, celestial objects could also be used for determining a position at sea. Different methods were then derived to find a Line-of-Position from a measured Altitude. This procedure is called "Sight Reduction". The first of such methods was developed in 1835 by the American captain Thomas Sumner. The method of finding a position from a measured Altitude used today, is called "Altitude-Intercept Method" and it was developed in 1875 by the French navy commander Adolphe-Laurent-Anatole Marcq de Blonde de Saint-Hilaire. This technique is based on calculating the Altitude of a celestial object at the estimated position and compare this calculated Altitude (Hc) with the measured Altitude (Ho) of that object. The Altitude difference (intercept = Hc - Ho) is directly related to the distance between the estimated position and the location of observation, eventually yielding a Line-of-Position (LoP).

The Principle of Celestial Navigation

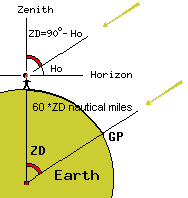
The Altitude of a celestial object Ho is the angle - measured by an observer on Earth - between the object and the horizontal plane in the location of the observer. If a celestial object is in the Zenith of the observer, its Altitude would be 90°. In this case, the observer would be at the GP of the object. If the observer is some distance away from the GP of the object, the measured Altitude is less than 90°. It will be less than 90° by an amount proportional to the distance from the GP. Any distance on Earth, translates into an angle by the following relation: 1 Nautical Mile = 1 minute of arc on a great-circle segment. In the same way angles translate into distances. The picture on the right shows the situation, in which the observer is a distance "ZD" away from the GP of the observed celestial object. If ZD is expressed in degrees, the distance in nautical miles is: Distance [nm] = 60 * ZD [°]

The Altitude Ho measured by the observer in a location, which is a distance ZD away from the GP of the observed celestial body will be:

  Ho [°] = 90° - ZD [°]

  ZD [°] = 90° - Ho [°]

The Zenith Distance ZD, resulting from a sextant measurement, is both the earth-bound angular distance between the GP of the observed celestial body and the location of the observer, as well as the angular distance on the celestial sphere between the position of the celestial object and the Zenith of the observer.

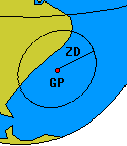All zenith points with a given "ZD" distance from a celestial object, are on a circle on the celestial sphere centred on the location of observed object. The radius of this circle - in degrees - is equal to "ZD". A similar circle on the Earth can be constructed. From any point on this circle, the observed Altitude "Ho" of this celestial object would have the same value. Hence, it is called Circle-of-equal-Altitude. Its center is the GP of the celestial object. The radius of the circle is the Zenith Distance "ZD". If also the Azimuth of the observed object (the direction referred to true North in which the object in the sky is sighted) could be measured, it would be possible to determine the observers position from a single observation.

On a moving vessel, it is not possible to measure the Azimuth with appropriate precision to use it for the determination of the position. The Azimuth Line must be drawn away from the GP towards the observer and as the radius of the Circle-of-equal-Altitude may be very large (one degree of Zenith Distance corresponds to 60 nautical miles), small errors on the Azimuth angle will result in large position errors. But by measuring the Altitude of another celestial body, a second Circle-of-equal-Altitude can be constructed (centred on the GP of a second celestial object). 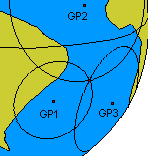Ordinarily, both circles would intersect in two widely separated points. One of these points would be the position of the observer. Ideally, a third observation will yield a unique position with the intersection of three Circles-of-equal-Altitude.

To put this theory into practice, a navigator measures the Altitudes of two or more celestial objects. Also the exact time (down to the second) at which the observations were done must be known. For this purpose accurate clocks called chronometers are needed. These are kept set to Universal Time (UT), as this is the time used in the Nautical Almanac.

The Nautical Almanac is a book of astronomical tables containing the positions (on the celestial sphere) of the Sun, the Moon, the planets and the stars used for celestial navigation. The positions are recorded in Declination and GHA. From these celestial positions, the Latitude and Longitude of the GP's of the sighted objects at the time of observation may be found.

Knowing the Altitudes of the observed objects and their GP's at the time of observation, the navigator - theoretically - has all the information necessary to construct the Circles-of-equal-Altitude from which eventually the position may be derived.

Actually, the navigator cannot plot the full circles - unless he is close to the GP of the observed celestial body. Otherwise, not only very large charts would be required, but also the latitude-dependent scaling factor of the Mercator chart must be taken into account. Due to this, a Circle-of-equal-Altitude will not be a circle in the projected chart - especially not if it covers a large range of Latitude. Circles-of-equal-Altitude cannot be easily constructed on a Mercator chart.
But fortunately, these Circles-of-equal-Altitude are usually so large that on reasonably scaled charts, only a small segment of the circle must be drawn. Moreover, the segments of these circles are so short that - without practical loss of accuracy - they can be drawn as straight lines. Like the lines obtained from bearings in piloting, a segment of a Circles-of-equal-Altitude is also called a Line-of-Position (LoP).

The Sumner Line-of-Position

Since Circles-of-equal-Altitude cannot be directly plotted on a nautical chart, methods had to be developed to obtain a Line-of-Position from a measured Altitude. This process is called "Sight Reduction" and is was only after these methods had been developed and established among navigators, that Celestial Navigation was augmented to a true method of navigation enabling of determining a position only by the measuring the Altitude of celestial bodies.

After chronometers became available and affordable for maritime navigation, a method called "time sight" was used to obtain the Longitude information from the Altitude of the Sun. One practical problem with the "time sight" is that it requires the knowledge of the Latitude, which had to be obtained from dead reckoning, which remained the primary navigation method throughout the 19th century.

In 1837, after having sailed 600 Miles through rain and fog over the Atlantic and entering the passage between Ireland and Wales, captain Thomas Sumner was able to measure a single Altitude during a short spell of sunshine. He then had to consider how to extract the most information possible of this single Altitude measurement to improve the knowledge on his position considering that his dead-reckoned Latitude would be very unprecise. For the problem posed by this situation he developed a new method of constructing a Line-of-Position for a measured Altitude, which enabled him a safe journey to his destination. Later, Thomas Sumner was able to derive a more general method for this method of Sight Reduction, which is still valid today. It is known as The Sumner Line-of-Position and starts from an assumed Latitude obtained e.g. by dead reckoning.

The Altitude-Intercept Method of St. Hilaire

About 40 years after Thomas Sumner had found his method to construct a Line-of-Position from an arbitrary Altitude measurement, an even more general method was developed by the French navy commander Adolphe-Laurent-Anatole Marcq de Blonde de Saint-Hilaire. The method is called "Altitude-Intercept Method" and after 1885 this became the most practical method to find a position by celestial observations.

The Altitude-Intercept Method starts from the fact that a navigator normally has a good estimation of his Assumed Position (AP) - e.g. by means of Dead Reckoning. From the knowledge of the celestial coordinates of a sighted celestial object, the navigator can calculate the Altitude and the Azimuth of the celestial object at the time of his observation in the Assumed Position. This process of calculating the Altitude (and Azimuth) of a sighted object for the time of observation at the Assumed Position is called "Sight Reduction". On the chart, the Assumed Position is plotted - if not already available through the Dead Reckoning navigation process. Through the Assumed Position, the Azimuth line may be drawn. This Azimuth line is the line of direction pointing to the GP of the sighted celestial object.

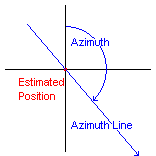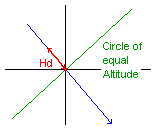
Perpendicular to the Azimuth Line a part of the - approximated - Circle-of-equal-Altitude can be drawn as a straight line. This line is a Line of Position if the navigator were exactly on the Assumed Position. In this case the measured - or "observed" - Altitude (Ho) would equal the calculated Altitude (Hc). If the observed Altitude (Ho) differs from the calculated Altitude (Hc), the altitude difference (Hd = Ho - Hc) can be used to translate the Circle-of-equal-Altitude (through the Assumed Position) along the Azimuth Line, such that the translated Circle of equal Altitude corresponds to the measured Altitude. The required translation is quite simple: the altitude difference (Hd), expressed in minutes of arc, is equal to the number of nautical miles by which the Circle-of-equal-Altitude has to be moved "up" or "down" the Azimuth Line. The sign of the altitude difference gives the direction ("away from" or "towards" the GP) in which the Circle-of-equal-Altitude must be moved. i.e. if the measure Altitude is greater than the calculated one by e.g. 13 minutes of arc, the Circle-of-equal-Altitude must be moved by 13 nautical miles towards the GP of the celestial object, and if the measured Altitude was less by e.g. 7 minutes of arc than the calculated one, the Circle-of-equal-Altitude must be moved away from the GP by 7 nautical miles.

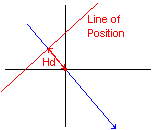
Finally the translated Circle-of-equal-Altitude (which must be approximated by a straight line at a right angle to the Azimuth Line) is the Line of Position (LoP), corresponding to the observed Altitude. As for each LoP, the navigator only knows that he is located somewhere on this line. A second LoP will eventually allow a position fix. The second "celestial" LoP may be obtained by a second observation of a different celestial object or by the observation of the same object a few hours later. Provided the navigator hasn't moved during his observations, he is at the intersection of the two LoPs. If the navigator has changed his position between two Altitude measurements, the original LoP has to be "advanced" over the direction and distance he has travelled (as in terrestrial piloting). The position will be at the intercept of the last LoP and the advanced - older - LoP.

As mentioned, the obtained Lines-of-Position are in fact circles centred around the Geographic Position of the observed object at the time of observation. These circles are usually so large that is suffices to draw the tangent to the circle as position line.

However, in tropical regions, where the Altitude can reach 90°, the circles can be very small! In this case it may well be possible to draw the Circles-of-equal-Latitude directly into the chart and a position can be obtained by the following method: take several observations when the Sun is nearly dead overhead (e.g. over a 15-minute period). For each observation, plot the coordinates (GHA,Dec) of the sub-solar point (GP) on the chart and draw a circle of radius equal to the Zenith Distance (90° - measured altitude). Over the 15-minute period you will probably have collected 3 or 4 observations, so you would be able to draw 3 or 4 circles who would all intersect (more or less) at one point. This method is simple but effective especially as in the tropics, Lines-of-Position usually end up running all almost North-South giving good Longitudes but bad intercepts and large errors in Latitude. In this situation, the traditional Noon Sight may be important to obtain reliable Latitude information.