Time

Time is essential to celestial navigation in its present form. The celestial bodies used as reference, are changing their apparent position in the sky in a continuous but predictable way. So while doing celestial observations and measuring the Altitude of celestial objects, the exact time of the measurement does matter! Roughly estimated - in tropical latitudes - an error of one second will result in a position error of 0.25 nautical mile (500 meter).

Therefore, an accurate board chronometer is a basic instrument for the celestial navigation. The Beagle (Charles Darwin's ship) carried 22 watches on board when she went around the globe in 1830.

Up until the 18th century when John Harrison developed the first prototype chronometer in 1720, no nautical instruments were available to "keep time" with a reasonable amount of accuracy. And until very recently, no earth-bound methods of time keeping could match the accuracy of time determinations derived from observations of the Sun and the Planets.

Our natural experience of time is particularly caused by the periodicity of astronomical phenomena: a year caused by the Earth's orbit around the Sun and the resulting run of the seasons, a month based on the motion of the Moon around the Earth and the change of the Moon phases, a day as the period of the Earth's rotation and the succession of day and night. Already in ancient times people tried to put some order in their domestic lifes and with the beginning of agriculture, a prediction of seasons was essential for survival. So, it is not surprising that time keeping and construction of calendars are among the oldest branches of astronomy.

Time and the Longitude Problem

Before the invention of accurate clocks, it was nearly impossible for sailors to find their exact Longitude and thus to find their exact position. In the days of Christopher Columbus and Francis Drake, Longitude could only be determined by "dead reckoning", estimating the travelled distance and direction. But this method was very not precise. Inaccurate sand glasses were used to determine travelling speed and travelled distance. Moreover the effect of magnetic deviation was not fully known until the 16th century, so also the travelled direction inherited a significant amount of inaccuracy.

If the local times at two points on Earth is known, the time difference is a measure to how far apart those points are in Longitude, East or West. This idea was very important to sailors and navigators throughout the centuries. They could measure the local time, wherever they were, by observing the Sun, but navigation required that they also know the time at some reference meridian, typically the Prime Meridian of Greenwich, in order to calculate their Longitude.

The only practical method for determining Longitude up to the 17th century was the method of timing lunar eclipses. The time of the eclipse for the reference meridian could be calculated in advance. Anyone who could observe this eclipse no matter of his position, would also exactly know the time at the reference meridian. This method had been in use since ancient times, but since eclipses are rare, it is of limited use.

Although accurate pendulum clocks existed in the 17th Century, the motions of a ship and changes in humidity and temperature would prevent such a clock from keeping accurate time at sea as required for navigation.

In 1675 King Charles II founded the Royal Observatory in Greenwich to solve the problem of finding Longitude at sea. The Greenwich astronomers first started to elaborate the following idea: if an accurate catalogue of the positions of the stars and the Moon could be made, and the position of the Moon relative to the stars could be measured accurately then by comparing this measured position with the compiled position of the catalogue, the Greenwich Time at the moment of the observation could be determined. So, the Moon's motion would be used as a natural clock to "measure" Greenwich Time from the position of the Moon relative to the background stars.
This means of finding Longitude was known as the Lunar Distance Method. Although this method was already discussed in the 16th century, the lack of accurate ephemeral data on the Moon, poor instruments, and the complexity of the necessary computations, prevented a breakthrough. Nonetheless in 1769-1770 Captain James Cook charted New Zealand with remarkable accuracy determining his longitudes only by lunar distances.

With the invention of the chronometer, by John Harrison in the early 18th century and it's further development, the accurate determination of Longitude was finally possible in a very simple way.

The work of the Royal Observatory in England and the developments in astronomy, led to increasingly accurate ephemeral data. In 1767 the English Nautical Almanac appeared. It compiled astronomical data collected by the Royal Observatory in a single source, and was developed specially for nautical navigation. This also established the Meridian of Greenwich as the Prime Meridian for measuring Longitude.

Because the ephemeral data from the Nautical Almanacs from the Royal Observatory was based on the local Greenwich time, the use of the Nautical Almanacs anywhere else on the world, also required a precise knowledge of the Greenwich (local) Time. Therefore the chronometers used for navigation on board of the military and mercantile vessels using the publications of the Royal Observatory would show Greenwich Time.

In the 19th century the Greenwich Mean Time (GMT) was introduced as a time basis for Nautical Almanacs world wide. In the 20th century this GMT was replaced by the Universal Time (UT). The time used in the Nautical Almanacs today is UT1 (see below).

Solar Time and Mean Solar Time

Until the 19th century, most European countries, even individual towns, used to the local solar time for their civil time keeping. The local solar time was based on a simple but well-defined astronomical measurement with a sundial. Sundials were positioned so that they indicated 12 o'clock, when the Sun was seen directly South (on the northern hemisphere), that is at the moment of Local Noon. The daily time scale was then adjusted such that 12 o'clock of this scale and Local Noon happened at the same time instance.
For many centuries civil time in the world was entirely based on this Solar Time. But by the end of the 19th century with the development of extended railway systems, the need for a more "synchronized" system of time keeping emerged.

Solar Time

The most natural "appearance of Time" is caused by the rotation of the Earth and the succession of day and night. Solar time follows this apparent revolution of the Sun around the Earth. A solar day is the interval between two successive passages of the Sun through the Local Meridian. Because in the course of a day, the Earth also travels a considerable part of its orbit around the Sun, a complete rotation with respect to the Sun lasts longer than a complete rotation with respect to the stars (sidereal day). Consequently, a solar day is longer by about 4 minutes than a sidereal day. A solar year and a sidereal year differ by one day.

A sundial displays the true solar time at its location, with Local Noon occurring if the gnomon cast a shadow that is parallel to the Local Meridian (North-South direction). Because the duration of the solar day (and thus the duration of a solar hour) varies over the seasons, the time before and after the 12'o clock noon line can only be roughly indicated. This variation is a consequence both of the eccentricity of the Earth's orbit and the obliquity of the ecliptic (the tilt of Earth's rotation axis): The Earth moves at different speeds in different parts of its elliptical orbit, according to Kepler's second law, hence the sun seems to move at different speeds along the sky. Even with a perfectly circular Earth orbit, the Sun would move evenly along the ecliptic but its projection onto the celestial equator would move at varying speeds. In spring and autumn, the Sun is close to the crossing points of ecliptic and celestial equator. Its movement from day to day therefore is slanted to the equator, the projected velocity is thus reduced. During summer and winter, however, the Sun is close to a vertex of the ecliptic and moves parallel to the celestial equator, making the projected velocity larger.

Both effects result in a variation of the length of a solar day over the seasons, with the shortest day (24 hours - 21.3 seconds) occurring around September 16th and the longest solar day (24 hours + 29.9 seconds) occurring around Decemper 22nd.

Mean Solar Time

To obtain a more uniform time scale, a fictitious "Mean Sun" is defined. This Mean Sun takes the same time from one vernal equinox to the next as the true Sun, but it is supposed to move with constant velocity along the celestial equator.

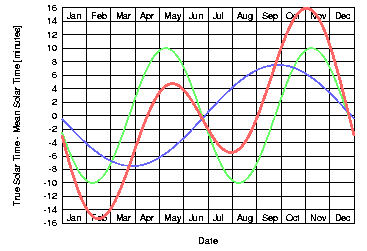
"Equation of Time"

The time difference between True and Mean Solar Time is called the "Equation of Time" and recorded over the year, it takes the form of the red curve sketched on the left. The green curve is the deviation of True and Mean Solar Time due to the obliquity of the ecliptic and the blue curve represents the effect of the eccentricity of the Earth's orbit. Because the two overlapping effects have different time scales (the eccentricity causes a period of one year, the obliquity of the ecliptic one of half a year), the Equation of Time (shown red) has two minima and two maxima per year (near Feb 12, May 15, Jul 27 and Nov 4). The maximum difference between True and Mean Solar Time is about 16 minutes (near Feb 12 and Nov 4). Around Apr 16, Jun 15, Sep 1 and Dec 25 the True and Mean Solar Time are identical. The Equation of Time is zero for these days.

The difference between the True and Mean Solar Time can also be obtained from the Nautical Almanac. Besides the ephemerides for each day of the year, the almanac also gives the culmination time of the Sun for the Prime Meridian of Greenwich (which is always around 12'o clock UTC). The difference between the Greenwich culmination time of the Sun and 12'o clock UTC for a specific day, is the value of the "Equation of Time" for that day.

Universal Time (UT) and Atomic Time (TAI)

The Mean Solar Time is the averaged True Solar time over the year making this time scale more uniform by eliminating the effects of the non-uniform revolution of the Earth around the Sun. Based on this Mean Solar Time is a civil time scale called Universal Time (UT).

Eventually, all "natural" time scales based on the rotation of the Earth will suffer from non-uniform and even non-predictable irregularities of the motion of the Earth such as the effects of precession and nutation, the effect of the tides and even atmospheric phenomena.

Therefore, as the demands on the precision of time references increased during the first half of the 20th century, especially for experiments related to physics and relativity theory, scientists started to created a high-precision measure of time, independent of any astronomical phenomena and highly reproducible.

Universal Time Coordinated (UTC)

Universal Time Coordinated (UTC) is a human invention just as TAI is. Both UTC and TAI are based on the SI second but instead of TAI, UTC is not a "continuous" time scale. TAI and UTC differ from each other by an integral number of seconds.
UTC can be seen as the link between the earth-rotation-bound time scale of UT and the atomic clock based TAI. It is relatively easy to manufacture highly precise clocks that will keep TAI or UTC, while the only "clock" keeping UT precisely is the Earth itself.

UTC is the time distributed by standard radio stations that broadcast time signals. It can also be obtained readily from the Global Positioning System (GPS) satellites. The difference between UTC and UT1 is made available electronically (Internet) and broadcast so that navigators can obtain UT1.

For practical Celestial Navigation the UTC time as distributed by radio stations is a good enough approximation of the UT1 time used in the Nautical Almanacs.

The time difference between both scales of time - by definition - is smaller than 0.9 seconds. As of Oct 2001, the UTC time is lagging the UT1 time by 0.1sec. More up-to-date information on this can be found in the latest issue of the IERS Bulletin A reports of the International Earth Rotation Service (look for the value "DUT1" in the first lines of the report).

Time Zones

Until the 19th century, most European countries, even individual towns, used to indicate the local time on the basis of a well-defined astronomical measurement with a sundial. However in the modern society emerging in the 19th century, it was recognized that it is not very practical, to have different time indications across a country. Also, there should not be too many different time zones on a continent.

So in 1894, the countries of Europe agreed to synchronize their watches (this means that they all show the same time), and to use a unified indication of time. Since then, in continental Europe, with a few exceptions, it is no longer necessary to correct your watch when passing from one country to another. All countries use the same time, which is referred to as Central European Time (CET).

Similar changes are made in many other regions of the Earth. The establishment of world time zones accounts for the fact that for any given moment of the day, the Sun is rising in one place on the Earth, is standing high in the South at noon for another place and is setting for a third place. Two places 15° of Longitude apart, have one hour difference in local Solar Time. Considering these astronomical facts, it makes sense to use different civil time scales at different places on the Earth.

Principally the earth is divided into 24 Time Zones and each Time Zone extends over 15° of Longitude. All places within the same Time Zone will use the same time called Local Time corresponding to the Mean Solar Time of the central Meridian of the Time Zone.

The Local Time of a Time Zone usually differs by an integral number of hours from Universal Time (UT), although sporadically other differences occur. For Time Zones East of Greenwich the Local Time leads Universal Time whereas the Local Time of Time Zones west of Greenwich lag Universal Time.
The Time Zone, which adopts UT as Local Time is principally centred on the Prime Meridian of Greenwich (from 7.5°E to 7.5°W).

Ultimately, the adoption of a Local Time scale is a political decision and is therefore handled differently in individual countries. More information on which Local Time is used in the different countries around the world can be found at http://worldtimezone.com/.

The current Date and Time situation in the different Time Zones and at the Date Line, can be seen in the Time-Zones Window.

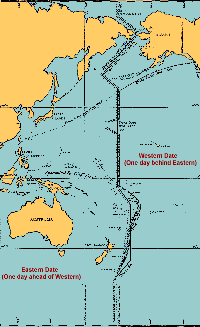
International Date Line

The International Date Line is the imaginary line on the Earth that separates two consecutive calendar days. The date in the eastern hemisphere (to the left of the line), is always one day ahead of the date in the western hemisphere. The International Date Line has been adopted as a matter of convenience and has no force in international law.

Without the International Date Line travellers going westward would discover that when they returned home, one day more than they thought had passed, even though they had kept careful record of the elapsed days. This first happened to Magellan's crew after the first circumnavigation of the globe (although this "circumnavigation's paradox" was already known since the 13th century). Likewise, a person travelling eastward would find that one day less had elapsed than he had recorded, as happened to Phileas Fogg in "Around the World in Eighty Days" by Jules Verne. The International Date Line can be anywhere on the globe. But it is most convenient to be 180° away from the Prime Meridian that goes through Greenwich, England. It also is fortunate that this area is covered, mainly, by empty ocean. Over the years, the position of the International Date Line has changed several times. Until 1845, the Philippines were East of the Date Line (the same side as the United States). It was on the eastern side because as a Spanish colony most Europeans arrived there via the Spanish colonies in South America. At the same time, Indonesia, which is almost directly to the South of the Philippines, was West of the Date Line because it was a Dutch colony and most European arrivals came via the Cape of Good Hope.

After the independence of the South American countries, most people travelling to the Philippines also came by way of the Cape of Good Hope, so it was decided to change from the East of the Date Line to the West of the Date Line.

Alaska, originally claimed by Russia, was to the West of the Date Line because most travellers arrived there by way of Siberia. When the United States bought Alaska in 1867 the Date Line was moved to the East of it.

The most recent change in the International Date Line was in 1995 when Kiribati moved a large segment of it to the East, so that the entire nation would be on the same side of the Date Line. As with all other changes in the International Date Line, this change was made by a local government to allow for local circumstances. As a result, the Date Line is as far East as E 150°, farther East than Honolulu.

The current Date and Time situation in the different Time Zones and at the Date Line, can be seen in the Time-Zones Window.