Latitude by Polaris

On the northern Hemisphere, the Pole Star (Polaris) has been a prominent beacon since the early days of maritime navigation. The current position of Polaris is very close to the North Celestial Pole (it was several degrees further away 2000 years ago). Today, Polaris seems to be on a fixed location on the night sky despite the rotation of the Earth, which makes all other celestial bodies apparently move on a circular path from East to West.
On the northern Hemisphere, Polaris will remain at an almost fixed position above the horizon. Moreover, the Altitude of Polaris is directly related to the Latitude of the observer. This was advantageously exploited by ancient navigators on land and sea.

Today, we know that the position of Polaris is not exactly on the North Celestial Pole. The current Declination (2018) is about 89° 20.1'. Translating the Polaris Altitude directly into Latitude may result in an error of up to 0.7° or a position error of up to 40 nautical miles in the North-South direction. As ephemerides became more accurate over the centuries, the measured Polaris Altitude, could be adjusted to obtain a better Latitude estimation.

This section describes how to determine Latitude from the Polaris Altitude and the procedure to apply and to calculate the required adjustments. The corresponding tables are printed on the last pages of the manual "Nautical Almanac for selected Stars" available from the Compiled Manuals - Download Section.

Latitude and the North Celestial Pole

As described above, a correction (actually it is an adjustment) on the measured Polaris Altitude is required because Polaris orbits in a small circle around the pole. When Polaris is at the exact same Altitude as the Celesital Pole, the correction is zero. At two points in its orbit it is at the same Meridian as the observer, either nearer than or beyond the Celesital Pole. At these points the corrections are maximum.

The exact correction value depends on several factors. The most important is the position of Polaris relative to the Observer. Other factors are the distance between Observer's Zenith and Polaris (which corresponds to the Observer's Latitude) and there is also a seasonal component.
In order to keep the correction table as simple as possible, these factors are considered as being independent. This approximation, allows to create some simple tables from which three correction components a0, a1 and a2 can be obtained. The tables are constructed such that the three correction factors are always positive. The complete calculation scheme is:

  Latitude = ( Ho – 1° ) + ( a0 + a1 + a2 )

Where Ho is the measured Polaris Altitude (corrected for dip and refraction) and the constant -1° is to compensate for the positive offset used in the three correction components.
As entry to the correction tables, the following information is required: LHA of Aries, DR latitude and the month of the year in which the observation is done.

The following example illustrates converting a Polaris sight to the observer's Latitude.
At 23h18m56s GMT, on April 21, 1994, at DR Latitude 50° 23.8' N, DR Longitude 37° 14.0' W, the observed altitude of Polaris (Ho) is 49° 31.6'.

To solve this problem, use the equation: Latitude = Ho – 1° + a0 + a1 + a2

Enter the Polaris table with the calculated LHA of Aries (162° 03.5'). The first correction, a0, depends only on the LHA of Aries. Enter the table column indicating the proper range of LHA of Aries; in this case, the "160°-169°" column. The numbers on the left hand side of the a0 correction table represent the integral degrees of LHA. Mental interpolation is applied to determine the proper a0 correction for the factional factor of LHA. The a0 correction for LHA = 162° is 1° 25.4' and the a0 correction for LHA = 163° is 1° 26.1'. In this case, the LHA fraction is 03.5', the a0 increment is about 1'. The interpolated increment for a 03.5' fraction is approximately zero. So, the a0 correction for 162° 03.5' is 1° 25.4'.

To calculate the a1 correction, enter the a1 correction table with the DR Latitude, in the 160°- 169° LHA column. There is no need for interpolation here; simply choose the latitude row that is closest to the Observer's DR latitude. In this case, 50°N. The a1 correction corresponding to an LHA range of 160°-169° and a latitude of 50°N is a1= +0.6'.

Finally, to calculate the a2 correction factor, keep the 160°-169° LHA column and enter the a2 correction table. Follow the column down to the month of the year; in this case, April. The correction for April is a2= +0.9'.

Sum the corrections, recalling that all three values are always positive. Subtract a constant 1° from the sum to determine the total correction. Finally, apply the resulting correction to the observed altitude of Polaris. This is then a good approximation of the observer’s Latitude.

  Tabulated GHA - (23h)         194° 32.7'
  Increment (18m56s)              4° 44.8'
  
  GHA                           199° 17.5'
  DR Longitude (-W +E)          -37° 14.0'
  
  LHA                           162° 03.5'
   
  a0 (162° 03.5') 	         +1° 25.4'      a0, a1 and a2 obtained from the Polars Tables
  a1 (Lat. = 50°N)                   +0.6'      with entries: LHA, DR Latitide 
  a2 (April)                         +0.9'      and Month of the year
  Sum 	                          1° 26.9'
  
  Observed Altitude 	         49° 31.6'
  Constant                       −1° 00.0'
  Total Correction               +1° 26.9'
  Latitude                     N 49° 58.5' 

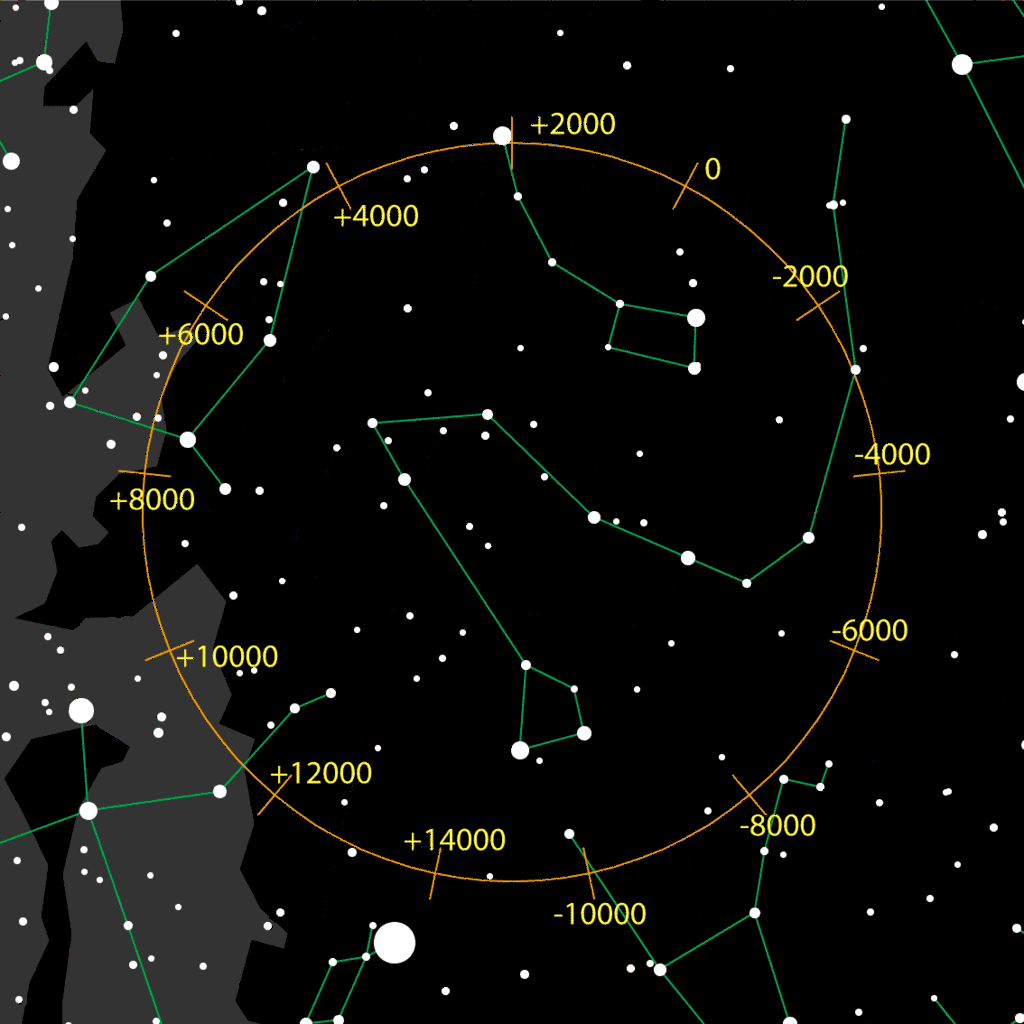
Position of the North Celestial Pole

The North Celestial Pole is the point on the Celestial Sphere to which the northern side of the axis of rotation of the Earth points to. But the Earth's axis of rotation is not fix with respect to the distant stars. Due to the effects of precession and nutation, the position of the North Celestial Pole moves on an approximately circular path around the North Celestial Pole. This is shown in the picture on the left. The precession movement has a period of about 26000 years, whereas the much smaller nutation movement (not shown here, because the associated amplitude is small) has a period of approximately 19 years. The numbers along the circular path of the North Celestial Pole correspond to the years according to the Gregorian Calender. Currently ("+2000"), the North Celestial Pole is very close to Polaris, which is the most prominent star in close proximity of the precession path. Brighter stars along this path, are Deneb ("+10000") and Vega ("+14000"), but none of them will ever come as close to the North Celestial Pole as Polaris does today.

Calculation of the Polaris Tables

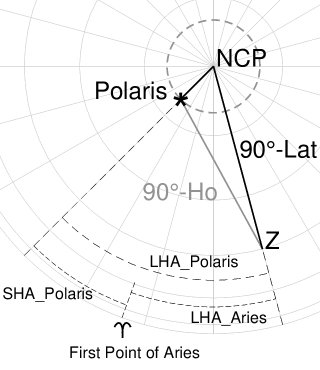
The picture on the right shows a part of the northern half of the celestial sphere. As indicated, Polaris apparently orbits in a small circle around the North Celestial Pole through the daily rotation of the Earth. In the picture, the circular orbit is exaggerated. In reality the radius of this circle is less than 1°. Also drawn in the picture, is the navigational triangle for a navigator at position Z, observing Polaris. The main angles of the triangle are defined by: the Declination of Polaris, the Latitude of the Observer and the Local-Hour Angle of Polaris (LHA_Polaris). Ho is the Altitude of Polaris as observed in the position Z (corrected for Dip and Refraction as in any other star sight). For the Polaris Correction Tables, not the LHA of Polaris, but the LHA of Aries is taken as main entry parameter. This is the meridian angle measured westward from the observer's Meridian to the Meridian of the First-Point-of-Aries. There is the following relationship between these angles: LHA_Polaris = LHA_Aries + SHA_Polaris LHA_Aries = GHA_Aries + Longitude (Observer) Both the values for GHA_Aries and SHA_Polaris can be found in the Nautical Almanac for Stars. For the Longitude, the estimated Longitude value for Z can be used.

The Polars Tables in the last part of the Nautical Almanac for Stars, are calculated as follows. First, the average values for the Declination and SHA of Polaris for the valid year are calculated. With these average celestial coordinates for Polars, the a0 corrections for all integral values of LHA_Aries are calculated assuming a Latitude value of 0° (observer at the Equator). The value for a0 is calculated from Ho of the navigational triangle: Ho = asin(sin(Lat)*sin(Dec)+cos(Lat)*cos(Dec)*cos(LHA_Polaris)). If Polaris were exactly on the NCP (Dec=90°), this value would be 0.0. Now we must add a0 to Ho to obtain the 0° latitude value: Ho + a0 = 0.0, and thus a0 = -Ho.
Further, for each 10° interval of LHA_Aries, the Ho value from the navigational triangle is calculated for different Latitude values. Taking the previously calculated a0 corrections into account the a1 value is obtained from: Latitude = Ho + a0 + a1 or a1 = Latitude - (Ho + a1).
Finally, for each 10° interval of LHA_Aries, the a2 values are calculated as an additional correction for a variation over the year (with the correct Declination and SHA for Polaris instead of the average values) also taking into account the appropriate a0 and a1 corrections: a2 = Latitude - (Ho + a0 + a1). The Latitude is fixed to 45° for this series of calculations.

The values for a0, a1 and a2 calculated as described above, can have positive or negative values. For doing the correction arithmetic, it is more convenient to have only positive numbers. This is obtained by adding 59.0 minutes to a0 and 0.5 minutes to a1 and a2, when they are tabulated. The total of 60.0 minutes "convenience" correction must be subtracted at the end of the correction scheme. Thus the complete scheme is: Latitude = Ho + a0 + a1 + a2 - 1, with a0, a1 and a2 corrections now all positive numbers.