Sail Away
Cover  <<  Sail Away  <<  Notes on Trigonometry  <<  .
 

Notes on Spherical Trigonometry

These notes are dealing with some principles of spherical trigonometry, which are relevant for practical navigation on a globe. Spherical trigonometry differs from plane trigonometry in the fact that the underlying tiangles are located on the surface of a sphere rather than on a plane.

In the following notes angles are assumed to be expressed in degrees. Also the basic trigonometric functions Sine (sin(x)) and Cosine (cos(x)) are assumed to take their argument (x) in degrees. This also inplies that the reverse functions Arcsine (asin(x)) and Arccosine (acos(x)) return angle values in degrees.

Some calculators will accept angle values only in radians. An angle value "adegree" expressed in degrees is converted into an angle value "aradians" expressed in radians the following identity: aradians = adegrees *3.1415/360 [radians/degrees].



The Oblique Spherical Triangle

 
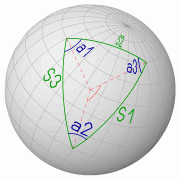sail042d_A.gif  
 A spherical triangle is defined by three sides with length S1, S2 and S3 and three including angles a1, a2 and a3.

The sides are segments of great circles and the length of each sides is defined by an angle. The angles of the sides are measured at the center of the sphere between the starting and ending "legs" of the great circle segment (shown red in the picture on the left).

The angles of the triangle a1, a2 and a3 are measured in the horizontal plane (on the surface of the sphere) of the vertex points of the spherical triangle.

Notice that since all elements (sides and intersection angles) of the triangle are defined as angles, the values of these elements do not depend on the radius of the underlying sphere.

In the next identities the following convention is assumed:
a1 is the angle opposite to side S1, a2 is the angle opposite to S2 and a3 is the angle opposite to S3.

Law of Sines:

  
  sin(a1)/sin(S1) = sin(a2)/sin(S2) = sin(a3)/sin(S3)


Law of Cosines for Sides:

  cos(S1) = cos(S2)*cos(S3) + sin(S2)*sin(S3)*cos(a1)
  cos(S2) = cos(S3)*cos(S1) + sin(S3)*sin(S1)*cos(a2)
  cos(S3) = cos(S1)*cos(S2) + sin(S1)*sin(S2)*cos(a3)

Law of Cosines for Angles:
 
  cos(a1) = -cos(a2)*cos(a3) + sin(a2)*sin(a3)*cos(S1)
  cos(a2) = -cos(a3)*cos(a1) + sin(a3)*sin(a1)*cos(S2)
  cos(a3) = -cos(a1)*cos(a2) + sin(a1)*sin(a2)*cos(S3)


Notice: Solving one of the above equations for a value of sides or angles of the spherical triangle, will require the inverse trigonometric functions Arcsine (asin(x)) and Arccosine (acos(x)). These "Arcus"-functions are defined uniquely only in a restricted range of resulting angles. This should be considered while applying these functions:

  • asin(x) is defined for x in the range between -1.0 to +1.0 and returns values between -90° to 90°. If y=asin(x) then also the angle "180°-y" is a valid value for the Arcsine of x: sin(180°-y) = sin(y) = x.

  • acos(x) is defined for x in the range between -1.0 to +1.0 and returns values between 180° to 0°. If y=acos(x) then also the angle "360°-y" is a valid value for the Arccosine of x: cos(360°-y) = cos(-y) = cos(-y) =x.



Law of Tangens for Angles:

If possible, a solution for the angles or sides should be formulated in the form of tangens (tan(x)) functions. The Arctangens function (atan(x)) returns values between -90° and +90° and can be used to handle the ambiquity of the Arcsine and Arccosine functions.

With a combination of the "Law of Cosines for Angles" and the "Law of Sines" the following identities can be deduced:

  tan(a1) = sin(S1)*sin(a3) / [cos(S1)*sin(S2) - cos(a3)*sin(S1)*cos(S2)]
  tan(a2) = sin(S2)*sin(a1) / [cos(S2)*sin(S3) - cos(a1)*sin(S2)*cos(S3)]
  tan(a3) = sin(S3)*sin(a2) / [cos(S3)*sin(S1) - cos(a2)*sin(S3)*cos(S1)]


The deduction will be explained for the angle "a1". Combine the first two equations of the "Law of Cosine for Angles":  
  cos(a1) = -cos(a2)*cos(a3) + sin(a2)*sin(a3)*cos(S1)                    (1)                
  cos(a2) = -cos(a3)*cos(a1) + sin(a3)*sin(a1)*cos(S2)                    (2)
with the first two equations of the "Law of Sines":
  sin(a1) = sin(a3)*sin(S1) / sin(S3)                                     (3)
  sin(a2) = sin(a3)*sin(S2) / sin(S3)                                     (4)
First replace the terms "sin(a2)" in Equation (1) with Equation (4), and the term "sin(a1)" in Equation (2) with Equation (3). Then replace the term cos(a2) in Equation (1), with the new Identity (2) and solve this new equation for "cos(a1)": 
  cos(a1) = -cos(a3)*[-cos(a1)*cos(a3) + sin2(a3)*sin(S1)*cos(S2) / sin(S3)] 
            + sin2(a3)*sin(S2)*cos(S1) / sin(S3)

  cos(a1) = cos2(a3)*cos(a1) - cos(a3)*sin2(a3)*sin(S1)*cos(S2) / sin(S3)
            + sin2(a3)*sin(S2)*cos(S1) / sin(S3)

  cos(a1)*[1 - cos2(a3)] = sin2(a3)*sin(S2)*cos(S1) / sin(S3) 
                         - cos(a3)*sin2(a3)*sin(S1)*cos(S2) / sin(S3)

  cos(a1)*sin2(a3) = sin2(a3)*[sin(S2)*cos(S1) - cos(a3)*sin(S1)*cos(S2)] / sin(S3)

  cos(a1) = [sin(S2)*cos(S1)-cos(a3)*sin(S1)*cos(S2)] / sin(S3)


Together with the "Law of Sines" identity used before: 
  sin(a1) = sin(a3)*sin(S1) / sin(S3)
the equation for the Tangens of "a1" can be written as:

  tan(a1) = sin(a1) / cos(a1) 
          = sin(a3)*sin(S1) / [ cos(S1)*sin(S2) - cos(a3)*sin(S1)*cos(S2) ]



The Right-Angled Spherical Triangle

If one of the angles a1,a2 or a3 is a staight angle (90°), the above reations can be simplified. Since any oblique spherical triangle can be described as either the sum or the difference of two right-angled spherical triangles, these simplified rules also provide a method for solving oblique spherical triangles.


Napier's Rules for Right-Angled Spherical Triangles

Given a right triangle on a sphere with the sides labeled S1, S2, and S3. Let a1 be the angle opposite side S1, a2 the angle opposite side S2, and a3 the right angle opposite to side S3. For this arrangement, John Napier (1550-1617) developed the following ten equations relating the sides and angles of this triangle (in which a3 does not show up since it is the fixed right angle):

  sin(S1) = sin(a1)*sin(S3) = tan(S2)/tan(a2)
  sin(S2) = sin(a2)*sin(S3) = tan(S1)/tan(a1)
  cos(a1) = cos(S1)*sin(a2) = tan(S2)/tan(S3)
  cos(a2) = cos(S2)*sin(a1) = tan(S1)/tan(S3)
  cos(S3) = cos(S1)*cos(S2) = 1/(tan(a1)*tan(a2))

The above Napiers Rules show only products and quotients of trigonometric functions, and are thus very suited for logarithmic computation. Actually, John Napier was also the first to developed the priciple of logarithms, and his work "Mirifici Logarithmorum Canonis Desciptio" of 1614 provided a complete practical toolbox for solving mathematical problems related to spherical triangles arising e.g. in navigation, astronomy and geodesy.



Cover  <<  Sail Away  <<  Notes on Trigonometry  <<  . .  >>  Applications last updated: 21-Mar-2017