Applications of Spherical Trigonometry in Navigation

These notes are dealing with some principles of spherical trigonometry, which are relevant for practical navigation on the globe.

As noticed before, in the following notes geometrical angles are assumed to be expressed in degrees. Also the basic trigonometric functions Sine (sin(x)) and Cosine (cos(x)) are assumed to take their argument (x) in degrees. This also implies that the reverse functions Arcsine (asin(x)) and Arccosine (acos(x)) return their values in degrees.

A location or position on the surface of the Earth is uniquely defined by means of Latitude (Lat) and Longitude (Lon), where Latitude is measured from the Equator to the North (positive) or to the South (negative) to the position and Longitude is measured from the Prime Meridian of Greenwich to the East (positive) or to the West (negative) to the position.

Similarly, the position of astronomical objects on the Celestial Sphere is determined by Declination (Dec), which is measured from the Celestial Equator to the North (positive) or to the South (negative) towards the celestial position and by Greenwich Hour Angle (GHA), which is always measured Westward from the Celestial Prime Meridian to the position of the celestial object.

The Terestrial Navigational Triangle

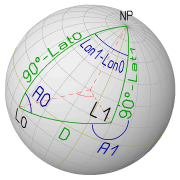
The identities for spherical triangles can be directly applied to the special-case triangle setup shown in the picture below. It consists of two arbitrary locations L0 (Lat0, Lon0) and L1 (Lat1, Lon1) and the North Pole (NP) as vertex points. These three sides are great-circle segments.
The vertex angles A0 and A1 are the angles under which the great-circle segment "L0 - L1" intercepts with the local Meridians in L0 and L1. The third vertex angle - at the North Pole - is the difference in Longitude of the two locations (Lon1-Lon0).

Since the North Pole is one of the vertex points, two of the sides are meridian segments and thus great-circle segments. The third side D is the great-circle distance between the locations L0 and L1. The meridian segments of the triangle are the complementary angles of the Latitudes of the positions L0 and L1: 90° - Latx. Two principal navigational problems can be solved with this spherical triangle arrangement: The "distance problem": If the locations L0 and L1 are known, the great-circle distance D between the locations as well as the angles A0 and A1 (true bearings) can be calculated. The "destination problem": If the location L0 (departure) and the great-circle distance D as well as the angle A0 are known, the position of the destination location L1 can be calculated.

The "Distance Problem": finding distance D and true bearings A0 and A1

 cos(D) = cos(90°-Lat0)*cos(90°-Lat1) + sin(90°-Lat0)*sin(90°-Lat1)*cos(Lon1-Lon0)

 cos(D) =      sin(Lat0)*sin(Lat1) + cos(Lat0)*cos(Lat1)*cos(Lon1-Lon0)

 D[°]   = acos[sin(Lat0)*sin(Lat1) + cos(Lat0)*cos(Lat1)*cos(Lon1-Lon0)]

This identity gives the "angular" distance D between the locations L0 and L1 in degrees. The distance expressed in nautical miles is obtained by the fact that along a great circle, one minute-of-arc corresponds to one nautical mile. So each degree of angular distance corresponds to 60 nautical miles:

 D[Nm]  = 60 * acos[sin(Lat0)*sin(Lat1) + cos(Lat0)*cos(Lat1)*cos(Lon1-Lon0)]

Notice:
The distance D is obtained by the Arccosine function (acos(x)) returning values between 0° and 180°, which is the expected range for D. Another valid mathematical solution for the acos(x) function is "360°-D", which corresponds to the great-circle segment "explementary" to the segment D.
In fact, the two locations L0 and L1 together with the North Pole, define two "complementary" spherical triangles. Both triangles together cover exactly a half-sphere of the Earth. This half-sphere is defined by the plane through L0, L1 and the center of the Earth. This plane also defines the great circle through L0 and L1 and also defines two great-cicle tracks between L0 and L1, one with distance D and the other "explementary" track with distance "360°-D" (or "21600nm - D" in nautical miles).

The values of the vertex angles A0 and A1 (shown as true bearings in the above picture) can be best obtained by the "Law of Tangens":

 tan(A0) = sin(90°-Lat1)*sin(Lon1-Lon0) / 
          [cos(90°-Lat1)*sin(90°-Lat0) - cos(Lon1-Lon0)*sin(90°-Lat1)*cos(90°-Lat0)]
         = cos(Lat1)*sin(Lon1-Lon0) / [sin(Lat1)*cos(Lat0) - cos(Lon1-Lon0)*cos(Lat1)*sin(Lat0)]

 tan(A1) = sin(90°-Lat0)*sin(Lon1-Lon0) / 
          [cos(90°-Lat0)*sin(90°-Lat1) - cos(Lon1-Lon0)*sin(90°-Lat0)*cos(90°-Lat1)]
         = cos(Lat0)*sin(Lon1-Lon0) / [sin(Lat0)*cos(Lat1) - cos(Lon1-Lon0)*cos(Lat0)*sin(Lat1)]

The angles A0 and A1 can also be deduced with the "Law of Sines", which yield simpler formulas, but with the disadvantage, that the results have an abiguity of 180° (since they are obtained from a Arcsine function). The advantage with the formulas deduced with the "Law of Tangens" is that they yield a unique result over the range -180° to +180°. For obtaining a valid true bearing, just add 360° to the negative values.

The identities for D, A0 and A1 are summarized below and are also implemented in an interactive JavaScript for calculating great-circle distances.

 D  = acos[sin(Lat0)*sin(Lat1) + cos(Lat0)*cos(Lat1)*cos(Lon1-Lon0)]

 A0 = atan2(cos(Lat1)*sin(Lon1-Lon0),sin(Lat1)*cos(Lat0) - cos(Lon1-Lon0)*cos(Lat1)*sin(Lat0))
 A1 = atan2(cos(Lat0)*sin(Lon1-Lon0),sin(Lat0)*cos(Lat1) - cos(Lon1-Lon0)*cos(Lat0)*sin(Lat1))

In order to steer the directions A0 and A1 as a course, the following must be considered: although both angles A0 and A1 refer to the "northern branch" of the local Meridian, they are only the initial starting courses to steer on the compass.
Great-circle sailing implies constantly changing steering courses, therefore, it is practiced only by large vessels, that are navigated by support of computers and GPS receivers. Navigators not having access to such sophiticated navigation equipment, may use a method of approximating a great-circle track by shorter rhumb-line tracks, which can be sailed by constant compass courses.

The "Destination Problem": Finding the Destination Location L1 (Lat1,Lon1)

If a great-circle journey is started from a location L0 in an initial direction A0 and the travelled distance is D, the coordinates of the destination location L1 can be found by solving the spherical triangle for the side "90°-Lat1" and the angle "Lon1-Lon0".

Applying the "Law of Cosines for sides" for "90°-Lat1" obtains the latitude of L1:

 cos(90°-Lat1) =  cos(90°-Lat0)*cos(D) + sin(90°-Lat0)*sin(D)*cos(A0)
 sin(Lat1)     =      sin(Lat0)*cos(D) +     cos(Lat0)*sin(D)*cos(A0)
     Lat1      = asin[sin(Lat0)*cos(D) +     cos(Lat0)*sin(D)*cos(A0)]

 tan(Lon1-Lon0) = sin(D)*sin(A0) /
                 [cos(D)*sin(90°-Lat0) - cos(A0)*sin(D)*cos(90°-Lat0)]
                = sin(D)*sin(A0) / [cos(D)*cos(Lat0) - cos(A0)*sin(D)*sin(Lat0)]

The summarized results yielding the coordinates of a destination (Lat0,Lon0) for a given departure (Lat0,Lon0), initial bearing (A0) and distance (D):

 Lat1 = asin[sin(Lat0)*cos(D) + cos(Lat0)*sin(D)*cos(A0)]
 Lon1 = Lon0 + atan2(sin(D)*sin(A0),cos(D)*cos(Lat0) - cos(A0)*sin(D)*sin(Lat0))

These identities for the destination location (Lat1,Lon1) are also implemented in an interactive JavaScript for calcutating the destination of a great-circle sailing.

The Celestial Navigational Triangle

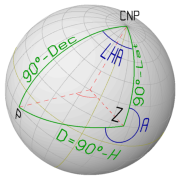
The celestial navigational triangle is used for solving the "Sight Reduction" problem in the construction of a Line-of-Position from a measured Altitude (Ho). This construction requires the calculation of the Altitude (Hc) of the observed body in the assumed position of the observer.
The "celestial" navigational triangle is very similar to the "terestrial" navigational triangle. The difference is that the underlying "globe" is the celestial sphere and thus also another coordinate system is used.

To calculate the Altitude of a celestial body, the following oblique triangle can be constructed on the celestial sphere: The vertices of the triangle are: the Zenith of the assumed position (Z), the position of the observed celectial body on the celestial sphere (P) and the Celestial North Pole (CNP) Two of the sides are segments of a Celestial Meridian with the Celestial North Pole as common point. The third side is the great-circle distance (D) between the position of the celestal body (P) and the Zenith of the assumed position (Z). This distance (D)is directly related to the "Height of the celestial body above the horizon" as measured in the location of the observer (H): D = 90° - H This identity beteen the distance P-Z and Altitude of a body (H) is the fundamental idea behind celestial navigation!

The celestial coordinates of the Zenith point (Z) are directly obtained from the terestrial coordinates of the assumed position (Lat,Lon): Dec_Z = Lat and GHA_Z = 360°-Lon.

The remaining elements of the Celestial Navigational Triangle are obtained as follows: The meridian segments of the triangle are the complementary angles of the Declination of the Zenith point (90° - Dec_Z) and of the Declination of the position of the celestial body (90° - Dec_P).
The top angle of the triangle - at the Celestial North Pole - is the difference in GHA between the Zenith of the observer and the position of the celestial body and called the Local Hour Angle (LHA = GHA_P - GHA_Z).

Altitude and Azimuth

Although, the position of the observer is unknown in the "navigation problem", an assumed position must first be used for the calculations. And in a next step, the correct location can be calculated from this assumed position. This method is known as "Altitude-Intercept Method" and was developed by the french navy commander Adolphe-Laurent-Anatole Marcq de Blonde de Saint-Hilaire at the end of the 19 th. century. It requires the calculation of Altitude (Hc) and the azimuth (Az) of a celestial body for the assumed position.

To calculate Hc and Az from the Celestial Navigational Triangle, the following is known:

• Assuming that the location of the observer is estimated, the position of the three vertices is known and thus the length of the two meridian segments is known.

• From the assumed position also the angle between the meridian segments - measured at the Celestial North Pole - is known (LHA).

Applying the "Law of Cosines" for sides, the angular distance D can be calculated, while the vertex angle A is obtained with the "Law of Tangens":

 D = acos[sin(Lat)*sin(Dec) + cos(Lat)*cos(Dec)*cos(LHA)]
 A = atan[sin(LHA)/(cos(Lat)*tan(Dec) - sin(Lat)*cos(LHA))]

For the "Altitude-Intercept Method" the Altitude Hc and the Azimith angle Az are required. These can both be derived from the angular distance D and vertex angle A: The distance D is the "co-altitude" so: Hc = 90° - D. The Azimuth angle must be derived from A and from the constellation: Az = A if Position of the sighted body is East of the Position of the observer or Az = 360° - A if the Position of the sighted body is West of the observer.

The correction for the Azimuth is necessary because the returned values of the atan(x) function are in the range 000° to 180°. This is because only the ratio of the sides of the underlying triangle is given to the atan(x) function. If however the values of each of the sides - with their correct sign - are known, the Arctangens can be calculated over the full range 000° to 360°. In many programming languages a function atan2(x,y) is implemented which performs this calculation. The input values x and y are the (signed) values of the sides of the underlying triangle.
If this function is used for calculating the Azimuth and if the LHA is calculated as LHA = -(GHA + Lon), the Azimuth Az will be calculated correctly without any further correction.

Summarizing, the computed altitude (Hc) and Azimuth (Az) for an observer located at (Lon,Lat) and a celestial object defined by it's celestial position (GHA,Dec) is obtained by:

 Hc = asin[sin(Lat)*sin(Dec) + cos(Lat)*cos(Dec)*cos(LHA)]

 Az = atan2[-sin(LHA),(cos(Lat)*tan(Dec) - sin(Lat)*cos(LHA))]       with LHA = GHA+Lon

 A  = acos[(sin(Dec) - sin(Lat)*sin(H))/(cos(Lat)*cos(H))]

LHA > 180°   Az = A
LHA < 180°   Az = 360° - A

When using this identity, the Azimuth angle Az is obtained from A by the following correction:
if (LHA > 180°) then Az = A else Az = 360° - A.

The above identities are implemented in an interactive JavaScript to calculate Altitude (Hc) and Azimuth (Az) of a Celestial Body for an Assumed Position.