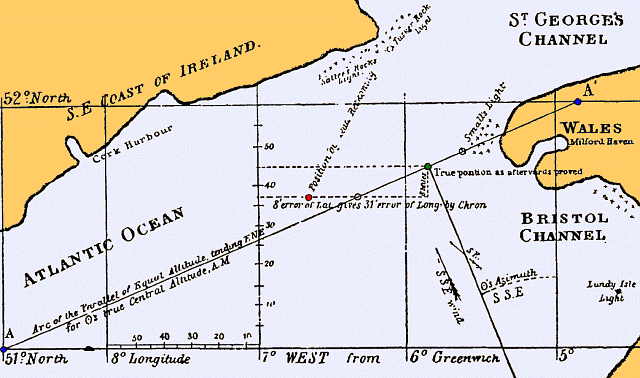
The Sumner Line-of-Position

In the first half of the 19th century, Captain Thomas H. Sumner developed a method to construct a Line-of-Position from a single Altitude measurement. He "conceived" this method more or less "forced by circumstances" in December 1837 while he was approaching the St. George's Channel between Ireland and Wales with only a deduced reckoning (DR) position and strong SSE winds setting his ship to the Irish lee coast. Heavy clouds had prevented taking any Altitudes for days. In the morning when they were already sailing the St. George Channel, the clouds cleared for a short instance and he was able to take the Altitude of the Sun. He then had to consider how to extract the most information possible of this single Altitude to improve the knowledge on his position.

Celestial Navigation in the beginning of the 19th Century

Prior to the development of Celestial Navigation, sailors navigated by "deduced" (or "dead") reckoning (DR). In order for this method to work, the navigator needed a way to measure both course and sailed distance. Course was measured by a magnetic compass, which had been known in Europe since at least the end of the 12th century. Distance was determined by a speed and time calculation. Speed was measured by "Heaving the Log" while time was measured with a sand glass.
Typically each half hour, the navigator would "heave the Log" and multiply the current speed of the vessel by the time travelled to get the sailed distance. Distances and courses were then thoroughly recorded in a "Logbook" and added over days and weeks to keep track of the current "deduced" position.
Dead Reckoning was still the primary navigation method as Captain Sumner sailed over the northern Atlantic to Scotland and that navigation crew in these days were indeed very skilled in DR navigation is demonstrated by the fact that after sailing more than 600 Miles, the offset in Sumner's position was only about 30 Miles, which implies an error of less that 5% in measuring speed, time and course. This is even more remarkable considering the variable weather, sea and sailing conditions including short-hauled passages and tidal currents in the North Sea.

The Noon Sight

The first "Celestial" methods for marine navigation enabled the determination of Latitude by measuring the Altitude of the Sun or the Moon at the moment it passed the local Meridian. For the Sun this happens at Local Apparent Noon ("Noon Sight"). For this method, only the Declination of the sighted celestial body for that day had to be known. Another popular method, was to determine the Altitude of Polaris during twilight and do some correction, because the position of Polaris is not exactly on the Celestial North Pole.
Altitudes were first measured with an Astrolab or a Cross Staff. Later Backstaffs or Octants were in use until about 1750 when the Sextant was invented. Because the determination of Latitude from a Noon Sight is simple and does not require keeping accurate time, it remained a well established method among navigators up to these days.

Longitude by Chronometer

The astronomical research performed at the Royal Observatory in Greenwich which was boosted by the invention of the telescope, ultimately led to increasingly accurate ephemeral data and in 1767 the first English Nautical Almanac appeared. The accurate Ephemeris enabled a new method to determine the mean solar Greenwich time by means of "lunar distances". Captain Cook managed to obtain an amazingly good charting of the Australian and New Zealand coasts using this method.
However, before the invention of accurate clocks, it remained nearly impossible for mariners to find their Longitude at sea. After the invention of the chronometer by John Harrison in the middle of the 18th century, marine chronometers were slowly being established as navigation instrument on seagoing vessels.

With this development, also the methods of finding the Position of a vessel a sea were slowly being improved further. The straightforward approach was to determine Latitude by the Noon Sight method and advanced by dead reckoning until the next Latitude by Noon Sight could be taken. Longitude could then be obtained from the (advanced) noon sight Latitude by taking the Altitude of a celestial body that was nearly due East or West. This method was called "Time Sight". One practical problem with the time sight is that it requires the knowledge of the Latitude. This dependency on Latitude is minimized if the sighted object bears nearly due east or nearly due west. But this is not always practicable.

The "Time Sight"

The most widely used sight-reduction method in the late 18th century and well into the 20th century was the "time sight". And the body most frequently used for this was the Sun. With the Altitude of the Sun the local apparent time at sea could be calculated, which could further be translated in Longitude. Originally Latitude was calculated in units of time, which gave the "time sight" its name.

If the Sun's Altitude (Hc) is measured and the observer's Latitude (Lat) is known or estimated (e.g. from an advanced Noon Sight), the Sun's Local Hour Angle can be calculated:

 LHA = acos([sin(Hc) - sin(Lat)*sin(Dec)] / [cos(Lat)*cos(Dec)])

The Declination (Dec) of the Sun was taken from the Nautical Almanac. The Sun's Local Hour Angle (expressed in units of "time") is directly related to the observer's local apparent time (LaT):

 LaT = 12:00:00 GMT - LHA   if the Sun is East of the local Meridian
 LaT = 12:00:00 GMT + LHA   if the Sun is West of the local Meridian

For calculating Longitude, the local apparent time must be translated into local mean time (LmT):

 LmT = LaT + EoT

The value EoT is the "Equation-of-Time" which is the time difference between Mean Time and Apparent Time on the Prime Meridian. This value varies from day to day and is listed in the Nautical Almanac.
The Local Mean Time at the ship compared to the GMT, which is the Mean Time of the Prime Meridian (and this again is the Chronometer Time used to do the Celestial Observations) will give the Longitude of the ship:

 Lon [°] = (LmT - GMT) [h] / 15 [°/hr]

In the times before chronometers became available, GMT had to be determined by the Lunar-Distance method.
The above explanations based on Apparent and Mean Solar Time are valid only for observations of the Sun. For other celestial bodies, the LHA has to be added or subtracted from the GHA of the body at the time the Altitude measurement was done.

The Sumner Line-of-Position

The scheme of determining Latitude by the Noon Sight and Longitude by a "Time Sight" was simple and well established on all seagoing vessels in the beginning of the 19th century. However, it had one basic flaw: an error in the obtained Latitude would also result in an erroneous Longitude. When the Altitude was taken around Noon, the error on Longitude could be very large, because the Parallel of Latitude and the Circle-of-equal-Altitude - obtained by measuring the Altitude - would intersect very unfavourable such that the error on Longitude can be considerably larger that the error on Latitude. If however, the Altitude is taken when the sighted object was due East or West, an error on Latitude would imply only a minor error on Longitude.

Also Captain Thomas H. Sumner was aware of these flaws when he tried to think how to make the best of his single Altitude observation at about 2 hours before Noon. He was worried about his position with the strong SSE winds setting him towards the Irish lee coast. His course at that moment was ENE. The position obtained with his DR Latitude and the "Time Sight", was East of his DR position (with the "Time Sight" method he used it could only be due East or West), which was further away from the coast than his DR Position. However, as a careful navigator, Captain Sumner was aware that the obtained Position included a considerable error on Latitude and an even larger error on Longitude. So he tried to figure out what would be the consequences of these inherent errors. Therefore, he tried to reduce his measured Altitude with an assumed Latitude 10 Miles further North (an thus closer to the lee-coast) and found a new Position that was even further East than the previous one. A third reduction with an assumed Latitude another 10 Miles further North, yielded a Longitude again further East than the two previous ones.
With these results on his chart, Captain Sumner realized that all three obtained Positions were on an straight line (which is in fact a small segment of a Circle-of-equal-Altitude). He also realized that this line must be the Line-of-Position from his Altitude measurement and that his vessel must be located somewhere on this line.

It was one of these unusual coincidences in history, that the obtained Line-of-Position not only was almost identical to his course line, but also this Line-of-Position was heading directly towards "Small's Rocks" lighthouse, which was a critical checkpoint off the west coast of Wales. So Captain Sumner concluded, that if he kept his course ENE along the obtained Line-of-Position, sooner or later "Small's Rocks" lighthouse would be sighted. Some time later the lighthouse was indeed discovered - despite the thick weather - and the voyage was then safely continued along the west coast of England.

Up to the time Captain Sumner by circumstances was forced to find a way to construct a "Celestial Line-of-Position", there was no established technique to do this. Astronomers and Cartographers knew that a measured Altitude resulted in a Circle-of-equal-Altitude and were even able to calculate a Position from the intersection points of two such Circles. But the underlying calculations were complex and had not become established among seafaring navigators.

Sumner's conclusion, that his method of constructing a "Line-of-equal-Altitudes" gives the true bearing of land was an important improvement in navigation techniques of his time. It enabled Navigators to make landfall at some identifiable point and then sail further along the coast to their final destination.

The Constructing of a Sumner Line-of-Position

In the beginning of the 19th century Natanial Bowditch developed and published some simplified calculation schemes for the "Time Sight". A combination of logarithmic arithmetic and trigonometric functions was used to to avoid multiplication and division in the required calculations and to minimize all together the number of required arithmetic operations. Besides the classical tables for the logarithmic and trigonometric functions, Bowditch also made use of special pre-calculated tables, which he published and updated in his "American Practical Navigator".

The method used by Captain Sumner for "reducing" his measured Altitude was known as "Bowditch's third Method" for determining apparent time and is derived in the following lines:

        cos(LHA) = [sin(Hc) - sin(Lat)*sin(Dec)] / [cos(Lat)*cos(Dec)] 
    1 - cos(LHA) = 1 - [sin(Hc) - sin(Lat)*sin(Dec)] / [cos(Lat)*cos(Dec)]
                 = [cos(Lat)*cos(Dec) + sin(Lat)*sin(Dec) - sin(Hc)] / [cos(Lat)*cos(Dec)]
                 = [cos(Lat)*cos(Dec) + sin(Lat)*sin(Dec) - sin(Hc)] / [cos(Lat)*cos(Dec)]
                 = [cos(Lat-Dec) - sin(Hc)] / [cos(Lat)*cos(Dec)]
 log(1-cos(LHA)) = log(cos(Lat-Dec) - sin(Hc)) + log(1/cos(Lat)) + log(1/cos(Dec))
                 = log(cos(Lat-Dec) - sin(Hc)) + log(sec(Lat))   + log(sec(Dec))

The Sine and Cosine functions were available as tables, but in order to be able to do the calculations with integer number values, the tabulated values were 100000 * sin(x) and 100000 * cos(x).
The calculation scheme would then look like:

 log(1-cos(LHA)) = log[100000*cos(Lat-Dec) - 100000*sin(Hc)] + log(sec(Lat)) + log(sec(Dec)) - 5

The right-hand side of this calculation was performed according to the following scheme (move the mouse over the picture to see the details of the calculation steps):

The LHA expressed as time was then obtained from a precomputed table implementing the function: LHA = acos(1-exp(X - 5))/15, with X the sum of logarithms of the above calculation scheme (first lines on the right hand side).

For constructing a Sumner Line, two integral Latitude values - one above and one below the DR latitude - were chosen. This avoided the complexity of interpolating between degrees for the Declination values from the Nautical Almanac. For each of the chosen Latitudes the "Time Sight" reduction was performed, eventually yielding two points of the Sumner's Line-of-Position.

Example

In the following, the Sumner Line is constructed from the data Captain Sumner obtained with his single Altitude measurement while sailing the St. George's Channel:
On 17th December 1837, sea account, the Latitude by DR was 51° 37'N. The Altitude of the Sun's lower limb, was 12° 02' at 10:47:13 Greenwich Mean Time by chronometer and the eye of the observer being 17 feet above the sea.

The Altitude of the Sun corrected for dip, refraction, semi-diameter and parallax is 12° 10'. The Latitude values chosen are 51°N and 52°N. The Longitude values for these assumed Latitudes are 008° 42'3W and 004° 49'5W respectively. This yields two points A (51°N,008° 42'3W) and A' (52°N, 004° 49'5W), which can be drawn in a mercator chart (Notice: the calculation scheme for the first point A is shown in the picture in the previous section). The Sumner Line-of-Position is the straight line joining these two points A and A' as shown in the map below.

As with any astronomical Line-of-Position, this straight line is an approximation of the circle-of-equal-altitude centered on the Georaphical Position of the Sun at the moment of the observation, with the Sun in the SSE direction in this case.

Sources