Terms and Conventions
Astronomy is the framework for Celestial Navigation and it
has been developed over the last 5000 years.
However, as most marine navigators had no real astronomical
background and were only interested in the practical use
of astronomical observations, they developed their own
system, which was good enough to solve their navigational
problems, but differs to some extend from the scientific
astronomical models.
In the next sections, the basic terms and conventions
used in the system of Celestial Navigation are summarized.
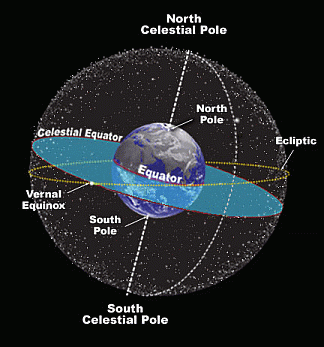
The Celestial Sphere
When discussing the position and motion of objects in the sky,
navigators like to pretend them to be attached to an imaginary
sphere surrounding the Earth.
This fictitious construction is called the Celestial Sphere.
It is centred around the Earth and depicts all celestial
objects as if they were at the same distance away from the Earth.
 |
|
Although this ancient geocentric model is not correct,
it is a simple and convenient way to describe the motions of
the stars and planets for an earth-bound observer.
We know today that a star's apparent brightness is determined
by its distance, as well as its physical size and temperature.
We also know that the stars' apparent motion through the sky
is due to the Earth rotation.
This rotational motion makes all celestial objects appear to
move together from East to West for any earth-bound observer.
And since the celestial objects are so far away from us, the
distance to them cannot be simply estimated so that they can
be imagined to be pinned to an imaginary sphere centred
around the Earth.
The Ecliptic is the apparent path of the Sun through the year,
plotted on the Celestial Sphere.
The plane of the Ecliptic is tilted about 23.5° against
the plane of the Equator.
This is because the rotation axis of the Earth is tilted 23.5°
against the orbital plane of the Earth around the Sun.
Twice a year - on the equinoxes - the Ecliptic crosses the
celestial equator.
The point on the Celestial Sphere at which the Ecliptic crosses
the celestial equator from south to north is called the
vernal equinox.
|
Coordinate System of the Celestial Sphere
Like the Longitude and Latitude system
on Earth, the Celestial Sphere can be provided with a coordinate
system to uniquely describe locations of stars and planets.
Note that there exists more than one coordinate system for
the Celestial Sphere.
The system described here is traditionally used for Celestial
Navigation and differs from the one used by astronomers in the
reference (the "celestial Prime Meridian") used for defining
the East-West coordinate.
The coordinate system of the celestial sphere consists of the
following components:
The celestial poles - the North Celestial Pole and
South Celestial Pole - are aligned with the poles of
the Earth (coinciding axis of rotation).
The Celestial Equator lies in the same plane that includes
the Earth's Equator.
And like the Earth's Equator, the Celestial Equator divides the
celestial sphere in a northern and southern celestial hemisphere.
Similar to the Meridians and Parallels of the Earth's coordinate
system, the coordinate system of the celestial sphere consists of
Hour Circles and Circles of constant Declination.
An hour circle is a great circle on the celestial sphere that
passes through the poles and intersects at right angles with
the circles of constant Declination.
Hour Circles are the meridians on the celestial sphere.
The Hour Circle passing through the Zenith of a Location on the
Prime Meridian of Greenwich is called Greenwich Hour Circle.
|
|

|
The angle between two arbitrary Hour Circles
(measured e.g. at one of the celestial poles) is called Hour Angle.
The Hour Angle is similar to a Longitude difference on the Earth.
The Hour Angle is called Local Hour Angle if the
Hour Circle passing through the Zenith of the observer is involved
and it is called Greenwich Hour Angle if the
Greenwich Hour Circle is involved.
The Declination (Dec) of a point on the celestial sphere is the
angular distance North or South of the celestial equator,
measured along the Hour Circle that passes through the point.
Declination on the celestial sphere corresponds to Latitude
on the Earth.
The Greenwich Hour Angle (GHA) of a point on the celestial sphere
is the angle between the Greenwich Hour Circle and the Hour Circle
of the point.
The angle is measured westward along the Celestial Equator
starting from the Greenwich celestial meridian - from 0°
through 360°.
The GHA differs from Longitude on the Earth in two aspects:
- Longitude is measured East or West - from 0° through 180°
- whereas GHA is measured West from 0° through 360°
- and in contrast to Longitude of a fixed location, the GHA of a fixed star
increases by about 15°/h due to the rotation of the Earth.
The following Table summarizes the equivalent terms of both coordinate systems:
| Terms of the Earth's coordinate system |
Terms of the Celestial Sphere |
| Equator | Celestial Equator |
| Latitude | Declination |
| Longitude (referring to Greenwich Meridian) | Greenwich Hour Angle |
| Longitude (referring to observer's Meridian) | Local Hour Angle |
| Longitude (angular E-W distance) | Hour Angle |
| Parallels | Circles of constant Declination |
| Meridians | Hour Circles |
| North Pole | North Celestial Pole |
| South Pole | South Celestial Pole |
| Location of the Observer | Zenith of the Observer |
The stars, pinned to the celestial sphere, turn around the Earth
keeping their relative position to each other.
This apparent fixed constellation is due to the fact, that the
stars are so far away from the Earth, that their relative motion
as seen from the Earth is very small (order of magnitude:
milliarcsec per year).
For the Sun, Moon and the planets, which are much closer to
the Earth, this is different: the Moon "moves" over the
celestial sphere (against the celestial background of stars)
with about 0.5° per hour.
The Celestial Poles, being in the axis of rotation, remain
fixed in the sky.
Also stars located near a celestial pole will appear to be
stationary in the sky.
That's the case for Polaris, a star that is near the
North Celestial Pole (its Declination is 89° 05' N).
Polaris is always in the North direction, a fact known by
every navigator in the northern hemisphere.
Near the South Celestial Pole there's no corresponding bright star.
The Zenith
The line connecting the center of the Earth with a location on the
surface of the Earth is called local vertical.
The local vertical of an earthbound observer, will eventually
extend to a point on the celestial sphere.
This point is called the Zenith of the observer.
So the Zenith is the point directly "overhead" of the observer.
The term "overhead" is defined by the direction of the local vertical.
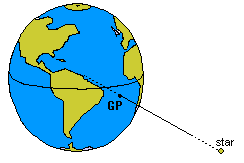
The Geographical Position of a Celestial Object
 |
Like the Zenith links the position of an earthbound observer
to a point directly overhead on the celestial sphere, the
Geographical Position links the location of celestial object
on the celestial sphere to a point on the surface of the Earth.
The Geographical Position (GP) of a celestial object is the
location on Earth for which the particular object is in the Zenith.
For each celestial object, the Geographical Position is a single
and unique location on the Earth, which can be found by drawing
an - imaginary - line from the center of the Earth to the center
of the particular object in the sky.
The location where this imaginary line passes through the surface
of the Earth is the Geographical Position of the celestial object.
An observer positioned in the Geographic Position of a star
will see this star directly in the vertical, above his head (his Zenith).
|
The Geographic Position of the Sun is also called the sub-solar point.
The Geographic Position of the Moon is the sub-lunar point and
that of a star its sub-stellar point.
Since the GP of a celestial object is located on the Earth,
it is expressed in Latitude and Longitude.
The GP can be easily calculated from the ephemerides
(celestial coordinates) of the celestial objects compiled
in the Nautical Almanac for each integral hour of the year.
Since the planes of the Equator and the Celestial Equator
are the same, the Latitude of the GP is equal to the
Declination of the celestial object.
The Longitude can be directly calculated from the GHA.
GP_Latitude = Declination
GP_Longitude = -GHA if GHA < 180°
= 360° - GHA if GHA > 180°
For understanding the principle of celestial navigation,
it is fundamental to recognize, that the Altitude of an
object measured with a sextant, is directly related to
the distance between the observer and the GP of the
observed celestial object:
Distance_from_Observer_to_GP = 90° - Measured_Altitude
Each Altitude measurement yields a distance to the GP of the
observed body and the resulting Line-of-Position is a Circle-of-equal-Altitude
centred on the GP.
This will be further elaborated in the next sections.
|