Tidal Predictions
Methods of Tide Prediction
The following is quoted from
http://en.wikipedia.org/wiki/Tide.
Isaac Newton's theory of gravitation first enabled an explanation of why there were
generally two tides a day, not one, and offered hope for detailed understanding.
Although it may seem that tides could be predicted via a sufficiently detailed
knowledge of the instantaneous astronomical forces, the actual tide at a given
location is determined by astronomical forces accumulated over many days.
Precise results require detailed knowledge of the shape of all the ocean basins
- their bathymetry and coastline shape.
Current procedure for analysing tides follows the method of harmonic analysis
introduced in the 1860s by William Thomson.
It is based on the principle that the astronomical theories of the motions of S
un and Moon determine a large number of component frequencies, and at each
frequency there is a component of force tending to produce tidal motion,
but that at each place of interest on the Earth, the tides respond at each
frequency with an amplitude and phase peculiar to that locality.
At each place of interest, the tide heights are therefore measured for a period
of time sufficiently long (usually more than a year in the case of a new port
not previously studied) to enable the response at each significant tide-generating
frequency to be distinguished by analysis, and to extract the tidal constants
for a sufficient number of the strongest known components of the astronomical
tidal forces to enable practical tide prediction.
The tide heights are expected to follow the tidal force, with a constant amplitude
and phase delay for each component.
Because astronomical frequencies and phases can be calculated with certainty, the
tide height at other times can then be predicted once the response to the harmonic
components of the astronomical tide-generating forces has been found.
The main patterns in the tides are:
- the twice-daily variation
- the difference between the first and second tide of a day
- the spring - neap cycle
- the annual variation
The Highest Astronomical Tide is the perigean spring tide when both the Sun and the Moon are closest to the Earth.
When confronted by a periodically varying function, the standard approach is to employ Fourier series,
a form of analysis that uses sinusoidal functions as a basis set, having frequencies that are zero, one,
two, three, etc. times the frequency of a particular fundamental cycle.
These multiples are called harmonics of the fundamental frequency, and the process is termed harmonic analysis.
If the basis set of sinusoidal functions suit the behaviour being modelled, relatively few harmonic terms need to be added.
Orbital paths are very nearly circular, so sinusoidal variations are suitable for tides
For the analysis of tide heights, the Fourier series approach has in practice to be made more elaborate than
the use of a single frequency and its harmonics.
The tidal patterns are decomposed into many sinusoids having many fundamental frequencies, corresponding
(as in the lunar theory) to many different combinations of the motions of the Earth, the Moon, and the angles
that define the shape and location of their orbits.
For tides, then, harmonic analysis is not limited to harmonics of a single frequency.[
In other words, the harmonies are multiples of many fundamental frequencies, not just of the fundamental
frequency of the simpler Fourier series approach.
Their representation as a Fourier series having only one fundamental frequency and its (integer) multiples
would require many terms, and would be severely limited in the time-range for which it would be valid.
The study of tide height by harmonic analysis was begun by Laplace, William Thomson (Lord Kelvin),
and George Darwin. A.T. Doodson extended their work, introducing the Doodson Number notation to organise
the hundreds of resulting terms.
This approach has been the international standard ever since, and the complications arise as follows:
the tide-raising force is notionally given by sums of several terms.
Each term is of the form
A*cos(w*t + p)
where A is the amplitude, w is the angular frequency usually given in degrees per hour corresponding
to t measured in hours, and p is the phase offset with regard to the astronomical state at time t = 0 .
There is one term for the Moon and a second term for the Sun.
The phase p of the first harmonic for the Moon term is called the lunitidal interval or high water interval.
The next step is to accommodate the harmonic terms due to the elliptical shape of the orbits.
Accordingly, the value of A is not a constant but also varying with time, slightly, about some average figure.
Replace it then by A(t) where A is another sinusoid, similar to the cycles and epicycles of Ptolemaic theory.
Accordingly,
A(t) = A*(1 + Aa*cos(wa*t + pa))
which is to say an average value A with a sinusoidal variation about it of magnitude Aa ,
with frequency wa and phase pa . Thus the simple term is now the product of two cosine factors:
A*[1 + Aa*cos(wa + pa)]*cos(w*t + p)
Given that for any x and y
cos(x)*cos(y) = 1/2*cos( x + y ) + 1/2*cos( x-y )
it is clear that a compound term involving the product of two cosine terms each with their own frequency
is the same as three simple cosine terms that are to be added at the original frequency and also at
frequencies which are the sum and difference of the two frequencies of the product term.
(Three, not two terms, since the whole expression is (1 + cos(x))*cos(y) ).
Consider further that the tidal force on a location depends also on whether the Moon (or the Sun) is
above or below the plane of the equator, and that these attributes have their own periods also
incommensurable with a day and a month, and it is clear that many combinations result.
With a careful choice of the basic astronomical frequencies, the Doodson Number annotates the particular
additions and differences to form the frequency of each simple cosine term.
Careful Fourier data analysis over a nineteen-year period (the National Tidal Datum Epoch in the U.S.)
uses frequencies called the tidal harmonic constituents.
 Nineteen years is preferred because the Earth, Moon and Sun's relative positions repeat almost
exactly in the Metonic cycle of 19 years, which is long enough to include the 18.613 year
lunar nodal tidal constituent.
This analysis can be done using only the knowledge of the forcing period, but without detailed
understanding of the mathematical derivation, which means that useful tidal tables have been
constructed for centuries.
The resulting amplitudes and phases can then be used to predict the expected tides.
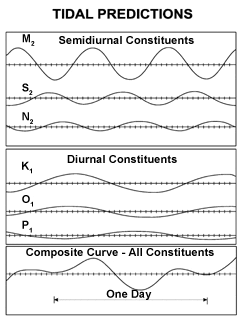
These are usually dominated by the constituents near 12 hours (the semi-diurnal constituents),
but there are major constituents near 24 hours (diurnal) as well.
Longer term constituents are 14 day or fortnightly, monthly, and semi-annual.
Semi-diurnal tides dominated coastline, but some areas such as the South China Sea and the Gulf of Mexico
are primarily diurnal.
In the semi-diurnal areas, the primary constituents M2 (lunar) and S2 (solar) periods differ slightly,
so that the relative phases, and thus the amplitude of the combined tide, change fortnightly (14 day period).
Nineteen years is preferred because the Earth, Moon and Sun's relative positions repeat almost
exactly in the Metonic cycle of 19 years, which is long enough to include the 18.613 year
lunar nodal tidal constituent.
This analysis can be done using only the knowledge of the forcing period, but without detailed
understanding of the mathematical derivation, which means that useful tidal tables have been
constructed for centuries.
The resulting amplitudes and phases can then be used to predict the expected tides.
These are usually dominated by the constituents near 12 hours (the semi-diurnal constituents),
but there are major constituents near 24 hours (diurnal) as well.
Longer term constituents are 14 day or fortnightly, monthly, and semi-annual.
Semi-diurnal tides dominated coastline, but some areas such as the South China Sea and the Gulf of Mexico
are primarily diurnal.
In the semi-diurnal areas, the primary constituents M2 (lunar) and S2 (solar) periods differ slightly,
so that the relative phases, and thus the amplitude of the combined tide, change fortnightly (14 day period).
In the M2 plot above, each co-tidal line differs by one hour from its neighbours, and the thicker lines show tides
in phase with equilibrium at Greenwich. The lines rotate around the amphidromic points counter-clockwise
in the northern hemisphere so that from Baja California Peninsula to Alaska and from France to Ireland
the M2 tide propagates northward.
In the southern hemisphere this direction is clockwise. On the other hand M2 tide propagates
counter-clockwise around New Zealand, but this is because the islands act as a dam and permit the tides
to have different heights on the islands' opposite sides.
(The tides do propagate northward on the east side and southward on the west coast, as predicted by theory.)
The exception is at Cook Strait where the tidal currents periodically link high to low water.
This is because co-tidal lines 180° around the amphidromes are in opposite phase,
for example high water across from low water at each end of Cook Strait.
Each tidal constituent has a different pattern of amplitudes, phases, and amphidromic points,
so the M2 patterns cannot be used for other tide components.
|
 Nineteen years is preferred because the Earth, Moon and Sun's relative positions repeat almost
exactly in the Metonic cycle of 19 years, which is long enough to include the 18.613 year
lunar nodal tidal constituent.
This analysis can be done using only the knowledge of the forcing period, but without detailed
understanding of the mathematical derivation, which means that useful tidal tables have been
constructed for centuries.
The resulting amplitudes and phases can then be used to predict the expected tides.
These are usually dominated by the constituents near 12 hours (the semi-diurnal constituents),
but there are major constituents near 24 hours (diurnal) as well.
Longer term constituents are 14 day or fortnightly, monthly, and semi-annual.
Semi-diurnal tides dominated coastline, but some areas such as the South China Sea and the Gulf of Mexico
are primarily diurnal.
In the semi-diurnal areas, the primary constituents M2 (lunar) and S2 (solar) periods differ slightly,
so that the relative phases, and thus the amplitude of the combined tide, change fortnightly (14 day period).
Nineteen years is preferred because the Earth, Moon and Sun's relative positions repeat almost
exactly in the Metonic cycle of 19 years, which is long enough to include the 18.613 year
lunar nodal tidal constituent.
This analysis can be done using only the knowledge of the forcing period, but without detailed
understanding of the mathematical derivation, which means that useful tidal tables have been
constructed for centuries.
The resulting amplitudes and phases can then be used to predict the expected tides.
These are usually dominated by the constituents near 12 hours (the semi-diurnal constituents),
but there are major constituents near 24 hours (diurnal) as well.
Longer term constituents are 14 day or fortnightly, monthly, and semi-annual.
Semi-diurnal tides dominated coastline, but some areas such as the South China Sea and the Gulf of Mexico
are primarily diurnal.
In the semi-diurnal areas, the primary constituents M2 (lunar) and S2 (solar) periods differ slightly,
so that the relative phases, and thus the amplitude of the combined tide, change fortnightly (14 day period).