Sight Reduction with Haversine Tables

Reformulating the Solution for the Navgational Triangle

The standard Law-of-Cosines solution of the navigational triangle is not very well suited for formulating a lean and simple calculation scheme:

  sin(Hc) = sin(Lat)*sin(Dec) + cos(Lat)*cos(Dec)*cos(LHA)

Besides sine and cosine table lookups, the above formula requires three time consuming and error prone multiplication operations. This is not suited for paper and pencil work.
Some work has been done since early 1800 to reformulate the standard solution e.g. using Haversine functions: hav(x) = sin²(x/2) = (1 - cos(x))/2   (note that hav(x) is always positive).

The Law-of-Haversine for the navigational triangle is (Davis):

  hav(Hc) = hav(Lat-Dec) + cos(Lat)*cos(Dec)*hav(t)

With t being the Meridian Angle. This formulation has no real benefit over the previous formula, but it can be further modified to further reduce the number of multiplications. In 1955 R. Doniol (see sources below) published a re-formulation with a single multiplication step for the Altitude and a division step for the Azimuth. This modified form of R. Doniol does not directly lead to a simpler calculation scheme but his work inspired others to elaborate an "all-Haversine-scheme" working scheme for both the Altitude and the Azimuth. Contributions to this were published 2013 through 2015 by H. Ix, G. Rudzinski and L. Bergman on the NavList discussion platform of the navigation community. The resulting re-formulation of the navigational triangle is as follows:

  hav(90°-Hc) =  hav(Lat-Dec) + [ 1 - ( hav(Lat-Dec) + hav(Lat+Dec)) ] * hav(t)

Again, 't' is the Meridian Angle and is directly related to the LHA between the Observer's Meridian and the Meridian of the Celestial Object. The right-hand side of the formula gives the Haversine value of the Zenith Distance ZD. But from this, the Altitude Hc, can easily be determined: Hc = 90°-ZD.

Similar to the first proposal of R. Doniol, also a re-formulation for the Azimuth Z can be elaborated:

 hav(Z) = [ hav(90°-Dec) - hav(Lat-Hc) ] / [ 1 - ( hav(Lat+Hc) + hav(Lat-Hc) ) ]

The corresponding calculation scheme for both Altitude an Azimuth is given below.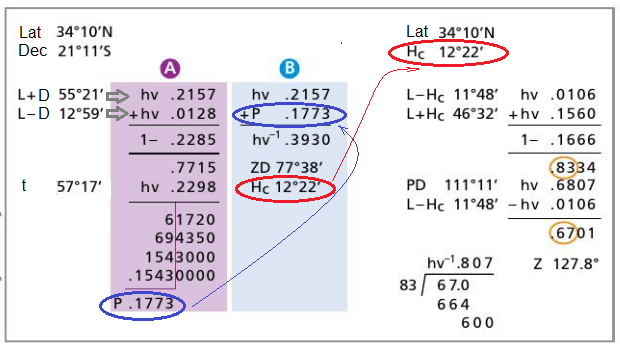

The Haversine Tables

When R. Doniol published his haversine solution for Sight Reduction, he also elaborated a haversine table that was conceived to be used with his proposed method. The original 'Doniol Table' as it is know today, also contained values for the Tangens and Cosine functions, which were part of the original Doniol scheme. However, the recently further developed scheme is based on an 'all-haversine' solution and the Tangens/Cosine part can be omitted.

Graphical Method

Especially the division step in the Doniol Azimuth scheme is tedious and uncomfortable. In 2015 Hanno Ix proposed a graphical method to determine the Azimuth with the 'all-haversine' scheme. The required accuracy for the Azimuth is not as high has for the Altitude, therefore a graphical method may effectively be used for this part of the Sight Reduction process.

Examples

In the following section, some examples of Sight Reduction using the Bygrave method are elaborated. The examples cover typical combinations of Assumed Position (N/S), Declination (N/S) of the celestial body and possible Meridian Angles. The operations that would be done using the Bygrave slide ruler in these examples are performed with an electronic calculator (see remark "(x)" above). The results are compared to the direct solution of the navigational triangle.

- to be completed soon ...

Sources