Lunar Distance

The "Lunar Distance Method" is a way of finding Greenwich Mean Time independent on the observer's location and through this, the Longitude of an arbitrary position on the Earth without the need for an accurate clock. Reliable marine chronometers were unavailable until the late 18th century and unaffordable until the 19th century. During this period of about one century (from about 1750 until 1850) mariners - such as James Cook - used the Method of Lunar Distances to determine Greenwich time needed to work out their Longitude.
The Lunar Distance Method is based on measuring the position of the Moon relative to the Sun, the Planets or stars on the Ecliptic. Since the Moon is close to the Earth compared to the other celestial objects, it's position chances relatively fast against the celestial background. The Moon orbits the Earth in 27.3 days relative to the stars and it's position as seen from the Earth, changes by about 13° a day or 33' per hour. So, although the Moon rotates from East to West as does the rest of the Celestial Sphere, the Moon is lagging this motion a little bit, making it "creep" slowly West to East compared to the background stars. In this sense, the position of the Moon relative to the celestial background, can be thought of as similar to the position of the hands of a clock relative to the dial and the current position of the Moon might be used to determine time similar as "reading" a chronometer. The stars along the Ecliptic would simply be the clock dial in the case of this "moon clock".
There are however some problems: the motion of the Moon with 0.5°/hr is very slow (compare this with the hour hand of a chronometer, which moves 30°/hr) and the time scale of the "moon clock" has no direct relationship with the chronometer time on the Earth. The first problem was tackled by instrument makers who constructed a precision optical instrument for measuring angles (the Sextant), whereas the second problem had to be tackled by astronomers and mathematicians who had to develop methods for precise prediction of the motion of the Moon. With the resulting Lunar Distance tables, the "Moon Time" can be translated into "Earth Time".

The principle of the "Lunar Distance Method" was first described in 1514 by Johan Werner, but was probably known before. But it took until the middle of the 18th century, before the motion of the Moon could be predicted accurately enough and instruments became precise enough for the method to be of any practical value.
Nevertheless, even with a modern sextant, the obtainable accuracy is rather limited. The average motion of the Moon along the Ecliptic is about 0.5' per minute. This is about the accuracy with which sextant measurements can be performed under ideal conditions. So the best that can be expected from the Lunar Distance Method is a time accuracy of 1 minute, which is sufficient to find Longitude within about 15 minutes of arc. However, on board of a ship in rough weather, this may as well be up to one degree of arc in accuracy or something like 60 miles of uncertainty in the obtained position.
It is also obvious that during the period of "new Moon", when the Moon is close to the Sun, no Lunar Distance observations can be performed.

History

One of the earliest tabulations of the positions of celestial bodies was "Ephemerides", compiled and published by the German astronomer Regiomontanus in 1474. In the early years of 1600, while studying the celestial observations of Tycho Brahe, Johannes Keppler was able to formulate his laws of planetary motion, which enabled significant improvements on the celestial model of Copernicus and better understanding of the motion of the planets. However, the accurate prediction of the motion of the Moon (a three-body gravitational problem without analytical solution) remained unsolved.
In 1753, the German astronomer Tobias Mayer published Lunar Tables of outstanding accuracy (based on a numerical solution of the three-body problem), enabling for the first time the determination of Longitude by the Lunar Distance Method with a precision that was within the limits set by the Longitude Act passed by the parliament of the United Kingdom in July 1714. From then on, the Lunar Distance Method became the only competing method for John Harrison's chronometer method for determining Longitude at sea.
When Mayer died in 1762, no decision had been reached in England concerning the "Longitude Problem". His improved Lunar Tables on which he had been working the last 7 years before his death, were tested by Nevil Maskelyne on a journey to Barbados in 1763, on which also the H4, the latest chronometer of John Harrison was tested.
Finally, on February 9,1765, the Board of Longitude advised the British Parliament that both Mayer and Harrison should be rewarded for their contributions to the solution of the longitude problem. But the Board signalled serious deficiencies in each of the two methods. Harrison's chronometer was not considered general enough, because it was not yet possible to produce accurate chronometers in sufficient quantities and Mayer's method was considered not practical because it entailed too much complicated calculation work.
Maskelyne who was one of the few people who had actually employed the Lunar Distance Method successfully at sea and had also been entrusted with the verification of Harrison's chronometer at Barbados, was convinced that the deficiencies signalled by the Board of Longitude were - at that time - much easier to overcome in the case of Lunar Distance Method than in the case of the chronometers. After he became Astronomer Royal at the observatory in Greenwich, he took up the plan to take as much as possible of the elaborate calculations away from the navigator at sea. This was accomplished by using pre-computed lunar distance tables that were already published (among other ephemeral data) in the first edition of the "Nautical Almanac" in 1767.
Pre-computed lunar distances were published in the "Nautical Almanac" until early 1900. Since the first half of the 19th century, chronometers were produced in sufficient quantities and at affordable prices such that they were used on board of an increasing number of ships. From this time on the method of Lunar Distances to determine Longitude gradually faded out, but remained useful for the required chronometer checks. By 1905, radio time signals were available as an independent time reference making the Lunar Distance Method more or less obsolete.

Determining Greenwich Time and Longitude with Lunar Distances

Practical measurements of Lunar Distances with the sextant will be performed by - seen through the sextant telescope - bringing the limb of the Moon in contact with the Limb of the Sun or in contact with a planet or an appropriate star (close to the Ecliptic). Having measured the Lunar Distance and the Altitude of the two bodies involved, the Greenwich Time is obtained in three basic steps:

• The limb-based measurements must be corrected for the semi-diameter of the involved bodies to obtain the observed (apparent) angular distance between the centers of the bodies.
• The apparent Lunar Distance is slightly affected by the effects of refraction and greatly affected by the effect of parallax. Because of the skewed angle that the Lunar Distance makes in the sky, these effects combine in a rather complex way. Allowing for these combined effects is a process known as "clearing the Lunar Distance".
• The cleared Lunar Distance must be compared with the prepared Tables of Lunar Distances to determine the time at which this distance will occur in order to find the Greenwich Time of the observation.

With the Greenwich Time found from the Lunar-Distance observation, the Longitude can be derived by comparing the Greenwich Time with the observed local time. The derived Greenwich Time can also be used to check the deviation of the chronometer used for the Lunar-Distance measurements.

A basic problem is that the measurements of the Lunar Distance and the two Altitudes must be preformed at the same time. Not a big issue in past days when the Navigator had some assistants at his disposal. If a single person has to do each of the three measurements there are two practical alternatives:

• the Altitudes can be measured before and after the measurement of the Lunar Distance and the corresponding values appropriately interpolated afterwards. In order to obtain reasonable results, the time span for all five (!) measurements should not exceed a few minutes.
• the Altitude values can be calculated from the estimated time and position. This method is favourable for land-bound exercising, because time and position may be known and the horizon may not be visible.

Measuring angular distances on the celestial sphere is different from measuring Altitudes. Instead of holding the sextant in the vertical plane, it must me held inclined, so that the instrument plane includes the center of the Earth and the two celestial objects (only under these conditions the Great-Circle distance between the objects is measured). A practical way to obtain such a measurement is to "rock" the sextant, to find the inclination that gives the lowest possible angle reading. Standing on a ship deck, this is challenging and requires some exercising.

Since the procedure of Lunar Distances is extremely sensitive to the accuracy of the measured angular distance between the Moon and the reference object, it is recommended to do a set of at least five successive measurements and to do a graphical or numerical averaging of the angle-time values to obtain a reliable measurement result.

Around the days of full Moon, care should be taken to use the "correct" - sharp - limb of the Moon and not the more blurred shadow line bordering the far side of the Moon.

Pre-Clearing the Lunar Distance

A Lunar-Distance measurement is always an indirect measurement in the sense that the distance from the Moon limb to the limb of the reference object is measured. However, the Almanac data generally refer to the geometrical center of the celestial bodies.
So, besides the correction for the Index Error, the measured Lunar Distance (LDsextant) has to be corrected for at least the semi-diameter of the Moon (and also for the Sun if that is used as the reference body) to obtain the "center-to-center" distance:

 LDapp = LDsextant ± SDmoon ± SDsun

The appropriate sign of the correction depends on which limb of the objects is chosen. For the "inner" limbs, the semi-diameter is added, for the "outer" limbs the semi-diameter is subtracted. It may be helpfull to draw a small sketch of the situation, especially if a combination of "inner"-"outer" limbs is used, which may be required with special moon constellations.

Corrections for the Augmentation of Semi-Diameter of the Moon

The semi-diameter for the Moon recorded in the Nautical Almanac is the value for the geo-centric position. If applied directly on the measured Lunar Distance (before a reduction to the geo-centric position), an additional correction for the effect called "Augmentation of the Moon's semi-diameter" must be applied.
With increasing Altitude of the Moon (Hmoon), there is a slight increase in the Moon's size - as observed on the surface of the Earth - due to the fact that the distance between observer and Moon decreases slightly if the Moon is high overhead.

The correction in Minutes-of-Arc is approximated by 0.3' * sin(Hmoon) and has to be added to the geocentric semi-diameter (SDmoon). The correction values can also be taken from the following table:

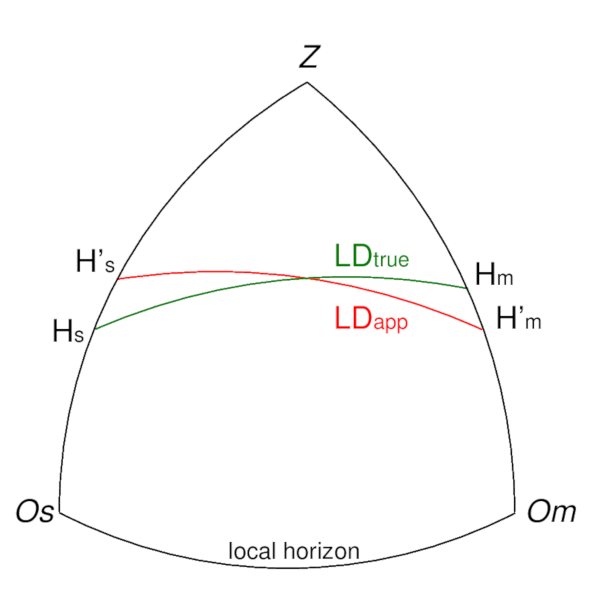
So the complete pre-clearing correction for the measured Lunar Distance is:

 LDapp = LDsextant ± (SDmoon + AUGMmoon) ± SDsun 

Correcting the measured Altitudes

Another part of the pre-clearing procedure is to perform the "standard" corrections for measured (apparent) altitudes, in order to obtain the true altitudes. These corrections are appropriate Index Error correction (IE), as well as corrections for Dip, Refraction, Parallax and semi-diameter (SD).

 H'm = H"m ± IE - Dip ± (SD_moon + AUGMmoon)
 H's = H"s ± IE - Dip ±  SD_sun

These are the apparent center-based Altitudes referring to the true horizon and these must be further processed to apply the corrections for refraction and parallax. These corrections are applied in two steps, because only the second part of these corrections will also affect the measured Lunar Distance.

 Hm = H'm - Refr_m + Prlx_m
 Hs = H's - Refr_s + Prlx_s

These are the true Altitudes with all corrections applied and referring to the center of the Earth. The differences (Hm - H'm) and (Hs - H's) will be required to elaborate how the apparent Lunar Distance (LDapp) will be affected by the effects of refraction and parallax.

Clearing the Lunar Distance

The pre-cleared Lunar Distance (LDapp) is the apparent "center-to-center" distance between the Moon and a reference body as observed from the surface of the Earth. As with the standard Altitude observations, this distance (angle) must be further corrected for the atmospheric disturbances (refraction) and then "reduced" to the geo-centric position taking into account the effects of parallax. This procedure is called "Clearing the Lunar Distance".

Mathematical Solution

The basic situation at the moment of the Lunar Distance measurement (after pre-clearing) is shown in the picture below. The observer obtained the Altitudes of the Moon (H'm) and the reference celestial body (H'r) as well as the pre-cleared distance (angle) between these objects LDapp (red segment). This yields three sides of a spherical triangle. Notice that the triangle is shown in the Horizontal Coordinate System of the Observer:

Z is the Zenith of the observer, the oposite side Om-Or is a segment of the local horizon defined by the position of the observer and the Azimuth Angles of the Moon (m) and the reference object (s). The segments Om-H'm and Os-H's are the observed (apparent) Altitudes. The angle Dapp is the observed (apparent) Lunar Distance. Additionally, a second triangle can be defined with the corrected (true) Altitudes Hm for the Moon and Hs for the reference object. Due to the parallax of the Moon being much larger than the refraction component, the observed Altitude of the Moon is smaller than the true Altitude of the Moon. The reference object for measuring the Lunar Distance will be a far away body (Sun, Planet or Stars) for which the parallax effect will be lower than the refraction component. In this case, the observed Altitude is larger than the true Altitude. The segments Om-Hm and Os-Hs are the corrected (true) Altitudes.

A solution of the above triangular problem to derive the true Lunar Distance (LDtrue), can be worked out starting with the fact that the two spherical triangles (H'm - Z - H's) and (Hm - Z - Hs) share the same (unknown) top angle in the Zenith (Om-Os), which can be cancelled from the double set of triangular relations.

For both triangles the top angle (Om-Os) can be calculated and then removed from the set of equations:

 cos(OmOs) = [cos(LDapp) - sin(H'm)*sin(H's)] / [cos(H'm)*cos(H's)]
 cos(OmOs) = [cos(LDtrue) - sin(Hm)*sin(Hs)] / [cos(Hm)*cos(Hs)]

Around 1770 Richard Dunthorne formulated the following awful form for the solution of the above set of equations (different other forms - equally awful - are also in use):

 cos(LDtrue) = [{cos(Hm)*cos(Hs)} / {cos(H'm)*cos(H's)} * 
                {cos(LDapp) - cos(H'm - H's)}] + [cos(Hm - Hs)]

With this, the true Lunar Distance (LDtrue), referring to the geo-centric position, can be calculated from the different Altitude and Distance values (apparent and true) obtained from the pre-clearing process. (LDapp, H'm, Hm, H's and Hs).

For an 18th-century Navigator, these calculations were quite impractical, so different schemes emerged to either formulate the solution in a way in which the multiplications could be solved with a logarithmic scheme or by using an approximation of reality, that still produced results with an accuracy suited for marine navigation.

In the following, two historically practised methods for clearing the lunar distance are discussed. One is the Borda Method and the other is the Merrifield Method. Borda's Method is analytical and calculates the exact true Lunar Distance. Merrifield's Method, is based on an approximation of the basic spherical triangles to get an approximated true Lunar Distance.

The Method of Jean de Borda for Clearing the Lunar Distance (1787)

Around 1787, Jean de Borda, a French mariner and scientist, formulated a logarithmic form of the distance clearing scheme derived above. In a first step an intermediate angle "phi" is calculated (with logsec() = -logcos()):

 logcos(phi) = 0.5 * { (logsec(H'm) + logsec(H's) + logcos((H'm + H's + LDapp)/2))
                    + logcos((H'm + H's - LDapp)/2) + logcos(Hm) + logcos(Hs) } 

 logsin(LDtrue/2) = 0.5 * { logsin(phi + (Hm + Hs)/2) + logsin(phi - (Hm + Hs)/2)}

The method of de Borda requires some number translations between linear and logaritmic as well as a large number of inspections in the (logarithmic) trigonometric tables.
A full description of the derivation of this calculation scheme can be found in "The Mathematics of the Longitude" written by Wong Lee Nah (National University of Singapore 2000-2001).

Here is how a possible worksheet for this method could look like (example):

  LDapp               79°38'6      79°38'6       -79°38'6
  H'm                 63°53'0                                 -logcos()   0.356350
  H's                 35°47'0                                 -logcos()   0.090854
  H'm+H's             99°40'0      99°40'0        99°40'0
                                 ---------      ---------
  H'm+H's +/- LDapp            A  179°18'6    B   20°01'4
  A/2                 89°39'3                                  logcos()  -2.220303
  B/2                 10°00'7                                  logcos()  -0.006664
 
  Hm                  64°17'0                                  logcos()  -0.362589
  Hs                  35°46'0                                  logcos()  -0.090763
  Hm+Hs              100°03'0                                           ----------
 (Hm+Hs)/2        C   50°01'5      50°01'5       -50°01'5                -2.233115 /2
  phi                 85°36'9      85°36'9        85°36'9   <- logcos()  -1.116558 
                                 ---------      ---------
                               D  135°38'4    E   35°35'4
  phi+C           D  135°38'4                                  logsin()  -0.155419
  phi-C           E   35°35'4                                  logsin()  -0.235093
                                                                        ----------
                                                                         -0.390512 /2
  LDtrue/2            39°38'1 *2                            <- logsin()  -0.195256 
  LDtrue              79°16'1 

With this scheme, the clearing of the Lunar Distance can be performed with a table based on the two functions "logcos()" and "logsin()", with logcos(90°-x) = logsin(x), so that in the end, only one of these two function must be tabulated. The negative numbers of the "logcos()/logsin()" functions can be avoided by replacing them with the "logsec()/logcsc()" functions and reformulating the calculation scheme accordingly.

The Approximation of John Merrifield for Clearing the Lunar Distance (1884)

This method is intuitive in its principle and is described here as an example of how an approximation for the clearing process might look like. However, the resulting calculation scheme seems to provide no significant simplification as compared to the Borda method. The great advantage is that in contrast to the previous methods, the true Lunar Distance is obtained by adding a correction to the apparent (measured) distance and not by multiplying the apparent Lunar Distance with a factor, which will be very close to 1, but bust be calculated with great accuracy and resolution. This then implies high resolution for the required tables, which is not necessary for the Merrifield method.

The simplification proposed by Merrifield is indicated in the picture on the right. The great-circle segment of the true Lunar Distance (LDtrue) is approximated by the segment x-y, which basically is the observed apparent Lunar Distance (LDapp) with some small corrections: H's-y for the Sun side and H'm-x for the Moon side.

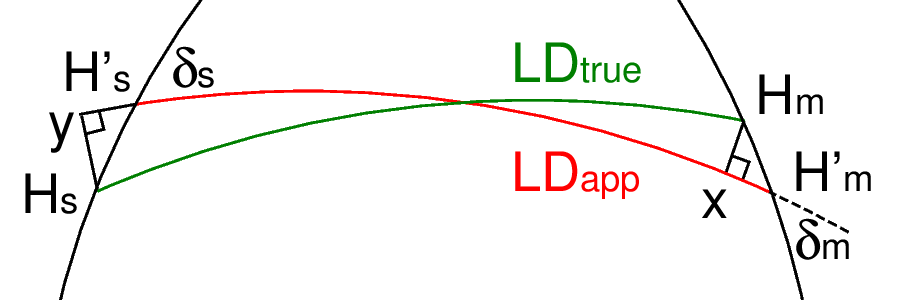
The Merrifield method is based on the fact that the mentioned corrections can be calculated from the small triangles H'm-x-Hm and H's-y-Hs, which can be approximated as plain triangles. The solution of these triangles requires two new variables: δm and δs, but it allows to formulate the true Lunar Distance in a compact form:

 LDtrue = LDapp + [(H'm - Hm)*cos(δm) + (H's - Hs)*cos(δs)]

In which the part in the square brackets [..], can be interpreted as the combined correction for parallax and refraction for both the Moon and the Sun (or another reference object). Notice that this combined correction term can be positive as well as negative (basically depending on the value of the Moon parallax).

The δ values can be calculated from the spherical triangle H's-Z-H'm using the law of cosines for the sides:

 cos(90°-H'm) =  cos(LDapp) * cos(90°-H's) + sin(LDapp) * sin(90°-H's) * cos(δs)

 cos(δs) = [ cos(90°-H'm) - cos(LDapp) * cos(90°-H's) ] / [ sin(LDapp) * sin(90°-H's) ]
         = [ sin(H'm) - cos(LDapp) * sin(H's) ] / [ sin(LDapp) * cos(H's)]

 cos(δm) = [ sin(H's) - cos(LDapp) * sin(H'm) ] / [ sin(LDapp) * cos(H'm)]

If a calculator with trigonometric functions is available, this is a most direct way of clearing the measured Lunar Distance from the effects of parallax and refraction. If the calculations have to be performed with trigonometric and logarithmic tables, the Merrifield approximation leads to a calculation scheme similarly complicated as the method of de Borda (or many other).

Conclusion

With the above described methods, a result for the true Lunar Distance at the moment of observation is obtained. The final step is to find the Greenwich Mean Time of the occurrence of this observed true Lunar Distance from the recorded values of the pre-computed Lunar Distance Tables.

Obtaining Greenwich Time from the Lunar Distance Tables

The final step to determine Greenwich Mean Time is to evaluate the Lunar Distance Tables. The Tables must be inspected to find the exact time at which the observed true Lunar Distance for the reference object occurs.
The exact Time is determined through linear interpolation of the tabulated (Time - Lunar Distance) pairs in which the true Lunar Distance is known. Notice that in order for this simple linear interpolation to be allowed, the time intervals of the tabulated data should not exceed a three hours span.

Current Position from Lunar Distance Measurement

After obtaining the Greenwich Mean Time, the Altitude measurements for the Moon and the reference object can be used to work out two Lines of Position and thus the current position can always be obtained simultaneously with the Greenwich Mean Time.

Pre-computed Lunar Distance Tables

Tables with pre-computed Lunar Distances for different reference objects used to be part of Nautical Almanacs up to early 1900. They allowed to compare cleared Lunar Distances from observations with recorded values and obtain Greenwich Mean Time from this comparison.

Selecting the Reference Object

The celestial reference bodies recorded in the daily pages of the tables are selected from the following objects: the Sun, the Planets and the brightest stars along the path of the Moon on the celestial sphere. This is the order of preference. Ideally, the reference object should have the same Declination as the Moon, but since this is usually not the case a certain amount of Declination mismatch must be allowed. From a rough analytical analysis, it can be concluded, that a Declination difference can be tolerated if the GHA distance is significantly larger than the Declination difference.

• The Sun: is selected if the difference in GHA is between 30 and 80 degrees
• The Planets: Mars, Venus and Jupiter are selected if the difference in GHA is between 30 and 60 degrees
• Bright Stars: are selected if the difference in Dec is lower than 10 degrees and the difference in GHA is between 30 and 60 degrees

The stars generally recommended for the lunar distance method are Sirius, Aldebaran, Altair, Antares, Fomalhaut, Hamal, Markab, Pollux, Procyon, Betelgeuze, Riegel, Regulus, and Spica, but other stars close to the ecliptic may be used as well, e. g., Enif.

Sources