Long-Term Ephemerides for the SunScope and Purpose
Due to the relative smooth and regular motion of the Earth around the Sun, compact
long-term ephemeris data for the Sun
can be compiled.
This section describes how such tables can be constructed and also how they are used.
These compact Sun Ephemeris tables may be used as a backup alternative if a
regular Nautical Almanac is not available.
The accuracy of the obtained GHA and Declination data is better than 3'. Background
Time is experienced in the first place by the rotation of the Earth
resulting in the day-night succession and in the second place by the
orbiting of the Earth around the Sun manifesting itself primary in
the succession of the different seasons over the year but also in the
changing star constellations at night.
However, there is no direct relationship between the time periods of
a day and a year.
For the Earth, it takes about 365.25 rotations to arrive at the same
position on it's orbit around the Sun. Construction of the TablesThe ephemeris data for the Sun is directly related to the orbit position of the Earth relative to the Sun. The basic idea behind the long-term Sun ephemeris tables, is to construct the data for a reference year and then to find the orbit position in the reference year corresponding to the situation at the time-of-observation for which GHA and Declination are to be evaluated. This "adjusted" orbit position will be expressed in units of time and is called Orbit Time. Table Layout
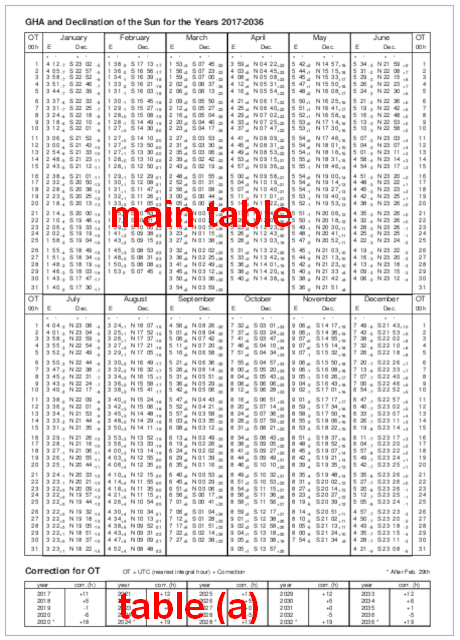
The main table,
supplies the basic ephemeris information. It uses Orbit Time as argument and gives
the values of the Equation-of-Time (E) and Declination (Dec) of the Sun for the start
of each day (00:00 UTC). These values are recorded for a one year time period.
This main table is constructed for a reference year, which may be chosen at about
half of the valid time range. The data for the other years is obtained by entering
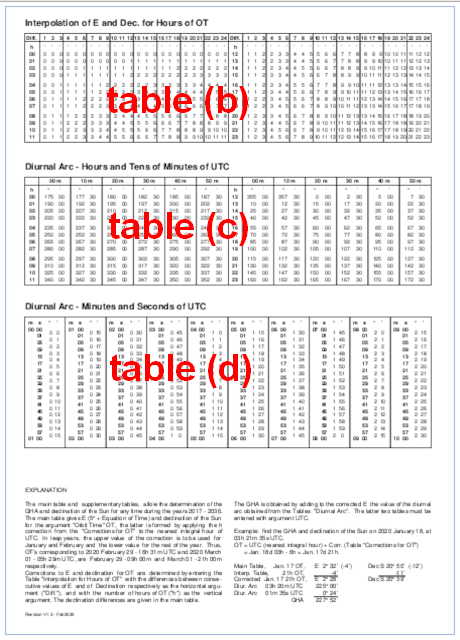
the main table with the correctly adjusted time for the Orbit Time. Adjusting the orbit position to the reference year, is sufficient to obtain the Declination value, but for obtaining the GHA information, also the rotation of the Earth must be considered. This requires the correct value for the Equation-of-Time (E) and the value of Diurnal Arc obtained from the table (c) and table (d) using the time-of-observation (in UTC) as argument. Explanation and Usage of the Tables
The first step to obtain the Sun Ephemerides for a UTC-time of observation
from the long-term table, is to determine the "Correction for OT" (h) from table (a).
This time correction is the time difference (in integral hours) between the year
of interest and the reference year for which the main table was compiled. ExampleGet the Sun Ephemerides for 2024, August 08, 17h 23m 44s UTC:
OT = UTC (nearest integral hour) + Correction (tab.a)
= Aug. 08, 17h + 18
= Aug. 09, 11h
Main table, Aug. 09, 00 OT, E 3° 35' (+3') Dec N 15° 58' (-18')
Interp. table (tab.b) 11 OT, +1' -8'
Corrected: Aug. 09, 11 OT, E 3° 36' Dec N 15° 50'
Diur. Arc (tab.c) 17h 20m UTC, 75°
Diur. Arc (tab.d) 03m 44s UTC, 0° 56'
GHA 079° 32'
The corresponding values for GHA and Declination, obtained from the 2024 Nautical Almanac are
079° 32.4' and UsageThe long-term Ephemerides for the Sun are primarily desiged to be used as backup solution for the more precise Nautical Almanac. Combining these long-term Sun Ephemerides, with the simplified Sight-Reduction Method as proposed by Robert Doniol, allows for a complete electronic-free method for Sun-based Celestial Navigation, which consists of only four pages of tables. These will fit in any sextant box and with the knowledge of how to use both the instrument and the required calculation schemes, a complete emergency navigation kit can be assembled. PrecessionThe procedure used here to construct the described long-term Ephemerides Tables for the Sun, does not account for the effect of precession, so that in the very long term some adaption to this procedure may become necessary. The reason is that the reference system slowly drifts due to precession. However, the basic principle to construct the Sun Ephemeris data as described above remains valid. In the rest of this section, a short introduction to the precession mechanism is given.
|
| Cover << Sail Away << Celestial Navigation << . | last updated: 25-Sep-2024 |
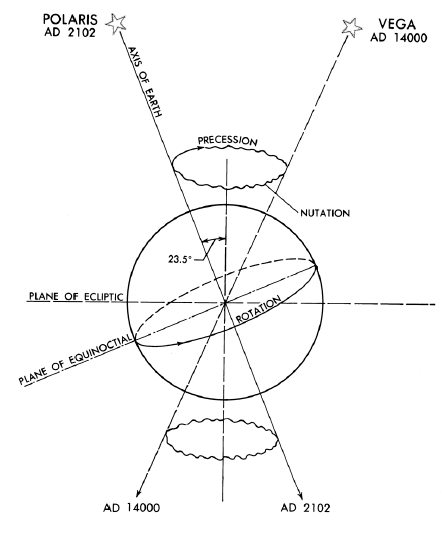 The axis of the Earth is undergoing a precessional motion similar to that of
a top spinning with its axis tilted. In about 25800 years the axis completes
a cycle and returns to the position from which it started. Since the celestial
equator is 90° from the celestial poles, it too is moving. The result is a
slow westward movement of the equinoxes and solstices, which has already carried
them about 30°, or one constellation, along the ecliptic from the positions
they occupied when named more than 2000 years ago.
The axis of the Earth is undergoing a precessional motion similar to that of
a top spinning with its axis tilted. In about 25800 years the axis completes
a cycle and returns to the position from which it started. Since the celestial
equator is 90° from the celestial poles, it too is moving. The result is a
slow westward movement of the equinoxes and solstices, which has already carried
them about 30°, or one constellation, along the ecliptic from the positions
they occupied when named more than 2000 years ago.