Position at 12:25 UTC on May 29. 2001
On May 29. 2001 we were sailing the ionian sea traveling from Levkas to
Paxos. This day was close to "half moon" so that in the early afternoon
both the Sun and the Moon were far above the horizon and two Lines-of-Position
(and thus a Position) could be obtained instantly from these two objects.
From the Nautical Almanac 2001 on the
May-29th page
it can be seen that the Culmination Times for Greenwich are about 6 hours
apart so that the Lines-of-Position should intersect at about 90°.
The "estimated" position was :
N 39° 10'3
E 020° 24'1
This position was taken from the GPS receiver to check the accuracy of the
celestial procedure.
The weather was hazy with some light cirrus clouds, but the limb
of both celestial objects could be clearly seen.
The sea was slight with light swell and wind 3 to 4 Bft from ENE.
The measured altitudes were:
object chronometer altitude limb
Moon: 12:25:40 29° 52'0 upper
Sun : 12:27:38 60° 12'7 lower
The measurements were obtained under the following conditions:
The chronometer was set to UTC time but had an error
of +11 seconds (the time shown on the chronometer lagged the real UTC
time by 11 seconds).
The chronometer is normally checked daily with a radio time signal.
In this special case, the time information of the GPS receiver was
used to determine the chronometer error. The index error (IE) was checked before and after
the altitude measurements and was 0'0 minutes of arc in both cases. During the measurements I was standing in the hatchway,
about 1.5 meters above the sea level. This implies a dip error of -2.2
minutes of arc (from the
"Correction Table for Dip"). Since the measurements were taken in a short time
interval (2 minutes) we assume no displacement between the measurements
(2 minutes with a speed of 5 knots would yield a displacement of
0.2 nm, which is well below the accuracy that can be
obtained with celestial navigation techniques).
Time of Observation
First the correct times of observation are recorded in the
Altitude Worksheet:
| Moon | | Sun |
|---|
Section 1 "Time of Observation"
Date 29 May 2001
Chronometer 12 h 25 m 40 s
Error + 00 m 11 s
__________________
Local Time ____h ___m ___s
Time Zone ± ____h
__________________
UTo 12 h 25 m 51 s
Object _ MOON __ upper
limb
|
needed only if
< chronometer set >
to local time
|
Section 1 "Time of Observation"
Date 29 May 2001
Chronometer 12 h 27 m 38 s
Error + 00 m 11 s
__________________
Local Time ____h ___m ___s
Time Zone ± ____h
__________________
UTo 12 h 27 m 49 s
Object _ SUN __ lower
limb
|
Since our chronometer is already set to UTC, local time and time-zone correction
are not used here. The results are the times of observation (UTo) in the
Universal Time system.
Observed Altitude
In this section the corrections on the measured sextant angles (Hs) are applied
(Section 2 of the Altitude Worksheet).
Beside the sextant altitude, the name of the sighted object and the approximate compass
direction are recorded. The value of the compass direction can be used to check the
calculated azimuth.
The index error was 0.0 minutes of arc and the dip correction is -2.2 minutes
of arc corresponding to an observation height of 1.5 meters above the sea
level.
For the refraction correction, the entries for 1030hPa / 30°C are used
(from the
"Correction Table for Refraction").
| Moon | | Sun |
Section 2 "Altitude"
Hs 29° 52'0 cel.obj. Moon
IE ± 0'0 app.dir. 225°
Dip - 2'2
________________
Ha 29° 49'8
SD - 16'1 lower limb: +
upper limb: -
Refr - 1'6
________________
29° 32'1
Prllx + 0° 48'4 HP 0° 59'3
________________
Ho 30° 20'5
|
Dip, Refr and Prllx
are found in the
Correction Tables
for
Sextant Altitudes
SD and HP are in the
Nautical Almanac
|
Section 2 "Altitude"
Hs 60° 12'7 sel.obj. Sun
IE ± 0'0 app.dir. 100°
Dip - 2'2
________________
Ha 60° 10'5
SD + 15'8 lower limb: +
upper limb: -
Refr - 0'5
________________
60° 25'8
Prllx + 0° 00'0 HP 0° 0'1
________________
Ho 60° 25'8
|
The next step is to find the geographical coordinates of
the sighted celestial objects at the time of observation. These coordinates
are required to further calculate the Altitude and Azimuth of these objects
at the estimated position.
Finally, the calculated Altitude (Hc) must be compared to the measured
Altitude (Ho) and the appropriated Line-of-Position can then be constructed.
Geographical Position of the Celestial Objects
in Section 3 "Nautical Almanac" of the
Altitude Worksheet
the Geographical Positions of the observed objects have to be elaborated.
For working out this section the
May-29th page
from the 2001 Nautical Almanac is required. From this page the GHA and Dec values
for 12:00 UTC are extracted as well as the increment values ddGHA and dDec
in the same line.
The procedure for the GHA looks like this:
| Moon | | Sun |
Section 3 "Nautical Almanac (GHA)"
GHA(NA) 270° 55'1 ddGHA -32'2
dHA +___° __'_ 15°/h
Interp ± __'_
________________
GHA ___° __'_ at time of obs.
|
May 29th
12:00
|
Section 3 "Nautical Almanac (GHA)"
GHA(NA) 0° 39'4 ddGHA -00'1
dHA +___° __'_ 15°/h
Interp ± __'_
________________
GHA ___° __'_ at time of obs.
|
For the GHA there are two interpolated values. The first value (dHA) is the
fraction of the hour after 12:00 UTC associated with a constant increase
of the GHA of 15°/h.
This value is found in the dHA columns of the
Interpolation Tables for Celestial Navigation.
For the Moon look into the 25Min/51Sec entry and for the
Sun look for the 27Min/49Sec entry. This yields the values
06° 27'7 for the Moon and 06° 57'2 for the Sun.
The sign of these first interpolation values is always positive.
The second interpolated value is associated with the additional increase
or decrease of the GHA (additional to the fixed 15°/h). To evaluate this,
the second (right) part of the "Nautical Almanac" section in the
Altitude Worksheet
is used:
| Moon | | Sun |
Section 3 "Nautical Almanac (GHA)"
Interpolation of Greenwich Hour Angle (GHA) |
Interp. Tab. |
Section 3 "Nautical Almanac (GHA)"
Interpolation of Greenwich Hour Angle (GHA) |
ddGHA 32'2 --> log(d) 32860
f 25' 51" --> log(f) 31906
+ _______
c=d*f/60 13'8 <-- 64766
|
column "p"
column "p"
column "s"
|
ddGHA 00'1 --> log(d) 9031
f 27' 49" --> log(f) 32225
+ _______
c=d*f/60 00'0 <-- 41256
|
Notice that this interpolation scheme does not take into account the correct sign
of the interpolated value (increment or decrement).
This sign of the result must be obtained from the ddGHA
value of the Nautical Almanac.
The interpolation results (-13.8 minutes of
arc for the Moon and -00.0 minutes of arc for
the Sun) are then used together with the looked-up interpolation results for
the 15°/h GHA increase, to obtain the correct GHA values for both the
Moon and the Sun:
| Moon | | Sun |
Section 3 "Nautical Almanac (GHA)"
GHA(NA) 270° 55'1 ddGHA -32'2
|
Interp + 6° 27'7 15°/h |
|
Interp - 13'8 <---
________________
GHA 277° 09'0 at 12:25:51 UTC
|
May 29th
12:00
|
Section 3 "Nautical Almanac (GHA)"
GHA(NA) 0° 39'4 ddGHA -00'1
|
Interp + 6° 52'2 15°/h |
|
Interp - 00'0 <---
________________
GHA 7° 31'6 at 12:27:49 UTC
|
The elaboration of the correct Declination values is similar to the GHA
procedure. The values for Dec and dDec from the Nautical Almanac are transferred
to the Worksheet and the dDec values are interpolated the same way as the
ddGHA values were interpolated. The result is the Declination of the Moon
and the Sun for the exact time of observation:
| Moon | | Sun |
|---|
Section 3 "Nautical Almanac (Dec)"
Dec N 14° 35'6 dDec -11'3
|
Interp - 04'8 <---
______________
Dec N 14° 30'8 at 12:25:51 UTC
|
May 29th
12:00
|
Section 3 "Nautical Almanac (Dec)"
Dec N 21° 40'2 dDec +00'4
|
Interp + 00'2 <---
______________
Dec N 21° 40'4 at 12:27:49 UTC
|
The interpolation scheme for the Declination is shown in the following table.
Notice that the conversion for the hour fractions (25' 52" and
27' 49") have already been looked up while interpolating
the ddGHA values and can be reused:
| Moon | | Sun |
Section 3 "Nautical Almanac (Dec)"
Interpolation of Declination (Dec) |
Interp. Tab. |
Section 3 "Nautical Almanac (Dec)"
Interpolation of Declination (Dec) |
dDec 11'3 --> log(d) 28325
f 25' 51" --> log(f) 31906
+ _______
c=d*f/60 04'8 <-- 60231
|
column "p"
column "p"
column "s"
|
ddGHA 00'4 --> log(d) 14150
f 27' 29" --> log(f) 32172
+ _______
c=d*f/60 00'2 <-- 46322
|
It is always good practice to double-check the interpolated results by doing
some simple inspections. The hour fraction can be rounded to the next quarter
of an hour and then the result of the interpolation should be close to 1/4th,
2/4th, 3/4th or 4/4th of the ddGHA/dDec value. In this example the hour fraction
is close to half an hour.
So, the interpolated values must be close to half the ddGHA/dDec values:
ddGHA(moon) ddGHA(sun) dDec(moon) dDec(sun)
full-hour -32'2 -00'1 -11'3 +00'4
interpolated -13'8 -00'0 -04'8 +00'2
Now, the Geographical Positions of the sighted objects
at the time of obervation is exactly known, and both the Altitude and the
Azimuth can be calculated for the location of the Estimated Position.
This process is called "Sight Reduction".
Sight Reduction
For the process of Sight-Reduction there are basically three alternative
methods:
- Use Tables of Altitude/Azimuth for pre-defined locations
(Worksheet available)
- The method of Ageton using logarithmic sine/cosine tables
(Worksheet available)
- Use an electronic calculator or special software applications
The electronic method can also consist of a web-based application such as
the
interactive Nautical Calculator.
This form will calculate the observers position from the known data:
Estimated Position, the Geographical Position of two sighted object and the
measured Altitudes.
The result from this application is ( N 39° 13.2' E 020° 23.0).
This position is about 3 nautical miles away from the GPS position.
This difference, which demonstrates the order of accuracy obtainable with
celestial navigation techniques, is principally due to measurement errors.
These inherent inaccuracies can be reduced by averaging a couple of measurements,
which is rather sumptuous, but also by practice! With some experience it
should be possible to make celestial fixes with an accuracy better that 2
nautical miles provided good measurement conditions (smooth sea, good visibility,
mid-range altitude, ...).
Without Nautical Calculator, the process of finding the position from the
observed altitude and Geographical Position (sight reduction) can
be performed with the precompiled Sight Reduction Tables.
The compiled Sight Reduction Tables
produce the Altitude and Azimuth Angle for integral degrees of Assumed
Position of the observer and Geographical Position of the sighted object
(select the appropriate table from the
Manual Download Section).
By choosing the appropriate Assumed position, both the Local Hour Angle
and the Latitude will be integer values.
The exact value of the Declination must be taken into account by
interpolating between two altitude values from the Sight Reduction Tables.
The procedure is as follows:
Choose an Assumed Position as close as possible
to the Estimated Position, such that both the Local Hour Angle as well
as the Assumed Latitude are integral degree values.
This has to be done separately for each observation. Use these new Assumed Positions as reference points
for the graphical evaluation of position on the plotting sheet. - Determine the calculated Altitudes and Azimuth Angles for both observations.
- Plot the Lines-of-Position in an appropriate plotting sheet.
In the above example, the Estimated Position and the Geographical Positions were:
Position 1 GP (moon) Position 2 GP (sun)
N 39° 10'3 N 14° 30'8 N 39° 10'3 N 21° 40'6
E 020° 24'1 277° 09'0 E 020° 24'1 007° 31'6
The corresponding Assumed Positions and input arguments for the Sight Reduction
Tables (shown in red) are (note that for the Assumed Position both Latitude and Longitude are changed):
Assumed Assumed
Position 1 GP (sun) LHA=GHA+Lon Position 2 GP (sun) LHA=GHA+Lon
N 39° 00'0 N 14° 30'8 N 39° 00'0 N 21° 40'6
E 020° 51'0 277° 09'0 298° 00'0 E 020° 28'4 007° 31'6 028° 00'0
With the above numbers marked in red and the correct part of the
Sight-Reduction manual
(Declination SAME as Latitude), the worksheet for this will be as follows.
For the Moon, the enties are: Lat=39°, Dec=14° and LHA=298°
Section 4 "Sight Reduction"
GHA 277° 09'0
E:+ W:-
LonAP + 020° 51'0 LatAP N 39° --> go to volume "30° - 39°"
________________ of the Sight Reduction Tables
Dec - Lat
LHA 298° Dec N 14° 30'8 SAME / CONTRARY
with Declination same as Latitude
N-Lat LHA>180°: Zc=Z
H 30° 24'9 dH +36'1 Ref 0° LHA<180°: Zc=360°-Z
S-Lat LHA>180°: Zc=180°-Z
Interp + 18'5 Z + 096°1 LHA<180°: Zc=180°+Z
________________ ________________
Hc 30° 43'4 Zc 096°1
Ho - 30° 20'5
________________
Hd 22'9
|
And the worksheet for the Sun with the following entries for the Sight-Reduction
tables: Lat=39°, Dec=21° and LHA=028°
Section 4 "Sight Reduction"
GHA 007° 31'6
E:+ W:-
LonAP + 020° 28'4 LatAP N 39° --> go to volume "30° - 39°"
________________ of the Sight Reduction Tables
Dec - Lat
LHA 028° Dec N 21° 40'6 SAME / CONTRARY
with Declination same as Latitude
N-Lat LHA>180°: Zc=Z
H 60° 00'7 dH +40'5 Ref 360° LHA<180°: Zc=360°-Z
S-Lat LHA>180°: Zc=180°-Z
Interp + 27'4 Z - 118°1 LHA<180°: Zc=180°+Z
________________ ________________
Hc 60° 28'1 Zc 241°9
Ho - 60° 25'8
________________
Hd 2'3
|
The values for H obtained from the Sight-Reduction Tables, must be improved by
interpolating dH for the correct Declination.
This is done similar to the interpolation of the Nautical Almanac data with the
Interpolation Tables for Celestial Navigation.
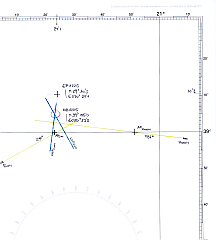
Line-of-Position
In the final section of the
Altitude Worksheet the data required to construct the Line-of-Positon is
assembled.
The obtained results from the Sight-Reduction procedure above,
(Hd=22'9 / Zc=096° for the Sun and Hd=2'3 / Zc=242° for the Moon as well
as the Assumed Position for both results) can be used to
draw two Lines-of-Position.
In this way a position from two celestial observations can be
elaborated graphicaly,
similar to the intersection of two bearing lines as used in terrestrial navigation.
For plotting the Lines-of-Position, a plotting sheet with a Mercator grid is required.
This is simply a blank nautical chart with a latitude-dependend ratio of the latitude-
to the longitude scale and can be constructed graphically or directly printed from
the appropriate page from the available
Mercator Plotting Sheets.
|
|
| 