The International Celestial Reference System (ICRS)

The International Celestial Reference System (ICRS) is the fundamental celestial reference system adopted by the International Astronomical Union (IAU) for high-precision positional astronomy. The ICRS, with its origin at the solar system barycenter and "space fixed" axis directions, is meant to represent the most appropriate coordinate system for expressing reference data on the positions and motions of celestial objects.

The definition and the creation of the International Celestial Reference Frame (ICRF) was a joint cooperative effort of a sub-group of the IAU Working Group on Reference Frames, which was formed expressly for the purpose of creating the definitive catalog of extra-galactic radio source positions using the best data and methods available at the time the work was done. The ICRF is the realization of the International Celestial Reference System (ICRS) at radio wavelengths. Monitoring the ICRS and maintaining its current realization, the ICRF, is the responsibility of the ICRS Product Center of the International Earth Rotation and Reference Systems Service (IERS).

Background

The ICRS is a set of specifications defining a high-precision coordinate system with its origin at the solar system barycenter and "space fixed" (kinematically non-rotating) axes. The specifications include a metric tensor, a prescription for establishing and maintaining the axis directions, a list of benchmark objects with precise coordinates for each one, and standard models and algorithms that allow these coordinates to be transformed into observable quantities for any location and time.

In this context, distinguishing between a reference system and a reference frame, as used in astronomy, is helpful.

• A reference system is the complete specification of how a celestial coordinate system is to be formed. It defines the origin and fundamental planes (or axes) of the coordinate system. It also specifies all of the constants, models, and algorithms used to transform between observable quantities and reference data that conform to the system.
• A reference frame consists of a set of identifiable fiducial points on the sky along with their coordinates that serves as the practical realization of a reference system.

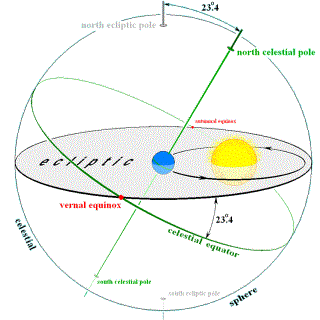For example, the fundamental plane of an astronomical reference system has conventionally been the celestial equatorial plane: the extension of the Earth's equatorial plane at some date, to infinity. The declination (Dec) of a star or other object is its angular distance north or south of this plane. The right ascension (RA) of an object is its angular distance measured eastward along the equator from some defined reference point where the right ascension value is set to zero.
This reference point, the origin of right ascension, has traditionally been the equinox: the point at which the Sun, in its yearly circuit of the celestial sphere, crosses the equatorial plane moving from south to north. The Sun's apparent yearly motion lies in the ecliptic, the plane of the Earth's orbit. The equinox, therefore, is a direction in space along the nodal line defined by the intersection of the ecliptic and equatorial planes; equivalently, on the celestial sphere, the equinox is at one of the two intersections of the great circles representing these planes. Because both of these planes are moving, the coordinate systems that they define must have a date associated with them; such a reference system must be therefore specified as "the Equator and Equinox of some date".

Of course, such a reference system is an idealization, because the theories of motion of the Earth that define how the two planes move are imperfect. In fact, the very definitions of these planes are problematic for high-precision work. Even if the fundamental planes are defined without any reference to the motions of the Earth, there is no way to magically paint them on the celestial sphere at any particular time. Therefore, in practice, we use a specific reference frame - a set of fiducial objects with assigned coordinates - as the practical representation of an astronomical reference system. The scheme is completely analogous to how terrestrial reference systems are established using survey control stations (geodetic reference points) on the Earth's surface.

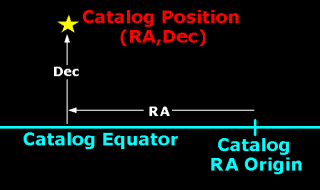Most commonly, a reference frame consists of a catalog of precise positions (and motions, if measurable) of stars or extra-galactic objects as seen from the solar system barycenter at a specific epoch (now usually "J2000.0", which is 12h TT on 1 January 2000). Each object's instantaneous position, expressed as right ascension (RA) and declination (Dec), indicates the object's angular distance from the catalog's equator and origin of right ascension. Any two such objects in the catalog therefore uniquely orient a spherical coordinate system on the sky - a reference frame.

A modern astrometric catalog contains data on a large number of objects (N), so the coordinate system is vastly overdetermined. The quality of the reference frame defined by a catalog depends on the extent to which the coordinates of all possible pairs of objects (approx. N²/2) serve to define the identical equator and right ascension origin, within the expected random errors. Typically, every catalog contains systematic errors, that is, errors in position that are similar in direction and magnitude for objects that are in the same area of the sky, or are of the same magnitude (flux) or color (spectral index). Systematic errors mean that the reference frame is warped, or is effectively different for different classes of objects. Obviously, minimizing systematic errors when a catalog is constructed is as important (if not more so) than minimizing the random errors.

To be useful, a reference frame must be implemented at the time of actual observations, and this requires the computation of the geocentric coordinates of the catalog objects at arbitrary dates and times. The accuracy with which we know the motions of the objects (unless they are assumed zero) is an essential factor in this computation. Astrometric star catalogs list proper motions, which are the projection of each star's space motion onto the celestial sphere, expressed as an angular rate in right ascension and declination per unit time. Because the tabulated proper motions are never perfect (even if assumed zero), any celestial reference frame deteriorates with time. Moreover, systematic errors i n the proper motions can produce time-dependent warpings and spurious rotations in the frame. Therefore, the accuracy and consistency of the proper motions are critical to the overall quality, utility, and longevity of reference frames defined by stars.

The positions of solar system objects can also be used to define a reference frame. For each solar system body involved, an ephemeris is used, which is simply a table or file of the celestial coordinates of the body as a function of time (or an algorithm that yields such a table). A reference frame defined by the ephemerides of one or more solar system bodies is called a dynamical reference frame. Because the ephemerides used incorporate the theories of motion of the Earth as well as that of the other solar system bodies, dynamical reference frames embody in a very fundamental way the moving equator and ecliptic, hence the equinox. They have, therefore, been used to align star catalog reference frames properly (the star positions were systematically adjusted) on the basis of simultaneous observations of stars and planets. However, dynamical reference frames are not very practical for establishing a coordinate system for day-to-day astronomical observations. The ICRS does not involve a dynamical reference frame.

Descriptions of reference frames and reference systems often refer to three coordinate axes, which are simply the set of right-handed Cartesian axes that correspond to the usual celestial spherical coordinate system. The xy-plane is the equator, the z-axis points toward the north celestial pole, and the x-axis points toward the origin of right ascension. Although in principle this allows us to specify the position of any celestial object in rectangular coordinates, the distance scale is not established to high precision beyond the solar system. What a reference system actually defines is the way in which the two conventional astronomical angular coordinates, right ascension and declination, overlay real observable points in the sky.

Late 20th Century Developments

The establishment of celestial reference systems is coordinated by the International Astronomical Union (IAU). The previous astronomical reference system was based on the Equator and Equinox of J2000.0 determined from observations of planetary motions, together with the IAU (1976) System of Astronomical Constants and related algorithms (Kaplan 1982). The reference frame that embodied this system for practical purposes was the Fifth Fundamental Catalogue "FK5" (Fricke, et al. 1988). The FK5 is a catalog of 1535 bright stars (to magnitude 7.5), supplemented by a fainter extension of 3117 additional stars (to magnitude 9.5). The FK5 was the successor to the FK3 and FK4 catalogs, all compiled from catalogs of meridian observations taken in the visual band (many such observations were, in fact, taken by eye). The formal uncertainties in the star positions of the FK5 at the time of its publication in 1988 were about 30-40 milli-arc-seconds over most of the sky, but the errors are considerably worse when systematic trends are taken into account.

Beginning in the 1970s, the most precise wide-angle (all-sky) astrometry was conducted not in the optical regime but at radio wavelengths, involving the techniques of Very Long Baseline Interferometry (VLBI) and pulsar timing. Uncertainties of radio VLBI antenna source positions listed in all-sky VLBI catalogs are now typically less than one milli-arc-second, and often a factor of ten better. Furthermore, because these radio sources are very distant extra-galactic objects (mostly quasars) that are not expected to show measurable intrinsic motion, a reference frame defined by VLBI positions should be "more inertial" (less subject to spurious rotation) than a reference frame defined by galactic objects, such as stars or pulsars. The VLBI catalogs do have the disadvantage that their origin of right ascension is somewhat arbitrary; there is no real equinox in VLBI catalogs, since VLBI has little sensitivity to the ecliptic plane. The VLBI origin of right ascension has effectively been carried over from one catalog to the next; it was originally based on the right ascension of the radio source 3C 273B measured using lunar occultations.

Because of the accuracy and stability of radio reference frames, since the mid 1980s, astronomical measurements of the Earth's rotation - from which astronomical time is determined - have depended heavily on VLBI, with classical methods based on star transits being phased out. Hence the situation evolved to where the definition of the fundamental astronomical reference frame (the FK5) became irrelevant to some of the most precise and important astrometric measurements. VLBI revealed, in addition, that the models of the Earth's precession and nutation that were part of the old system were inadequate for modern astrometric precision. In particular, the "constant of precession" - a measurement of the long-term rate of change of the orientation of the Earth's axis in space - had been overestimated by about 0.3 arc-seconds per century. Moreover, the success of the European Space Agency Hipparcos astrometric satellite, launched in 1989, promised to provide a new, very accurate set of star coordinates in the optical regime.

Thus, beginning in 1988, a number of IAU working groups began considering the requirements for a new fundamental astronomical reference system (Lieske & Abalakin 1990, Hughes et al. 1991). The resulting series of IAU resolutions, passed in 1991, 1994, 1997, and 2000 (IAU 1992, 1996, 1999, 2001), effectively form the specifications for the ICRS. The axes of the ICRS are defined by the adopted positions of a specific set of extra-galactic objects, which are assumed to have no measurable proper motions. The ICRS axes are consistent, to better than 0.1 arcsecond, with the Equator and Equinox of J2000.0 defined by the dynamics of the Earth. However, the ICRS axes are meant to be regarded as fixed directions in space that have an existence independent of the dynamics of the Earth or the particular set of objects used to define them at any given time.

The promotion, maintenance, extension, and use of the ICRS are the responsibilities of IAU Division 1 (Fundamental Astronomy), especially Commission 8 (Astrometry) and Commission 19 (Rotation of the Earth). The International Earth Rotation and Reference System Service (IERS), which was established by the IAU and International Union of Geodesy and Geophysics (IUGG), is also involved. The IERS generates VLBI-based science products for astrometry and geodesy, and the IAU entities provide a framework within the astronomical community for international collaboration, overall guidance for the work, and evaluation and endorsement of results.

ICRS Implementation

The Defining extra-galactic Frame

The International Celestial Reference Frame (ICRF or ICRF1) is a catalog of adopted positions of 608 extra-galactic radio sources observed with VLBI, all strong (greater than 0.1 Jy) at S and X bands (wavelengths 13 cm and 3.6 cm) (Ma & Feissel 1997). Most have faint optical counterparts (typically with visual magnitudes fainter than 18) and the majority are quasars. Of these objects, 212 are defining sources that establish the orientation of the ICRS axes, with origin at the solar system barycenter. Typical position uncertainties for the defining sources are of order 0.5 milli-arc-second. The orientation of the axes is defined from the ensemble to an accuracy of about 0.02 milli-arc-seconds. As described below, these axes correspond closely to what would conventionally be described as "the Equator and Equinox of J2000.0".

The International Earth Rotation Service (IERS) monitors the radio sources involved in the ICRF. This monitoring is necessary because, at some level, most of the sources are variable in both flux and structure, and the centers of emission can display spurious motions, which may not be linear on the sky or constant in rate (see the discussion in Ma et al. (1998), Section 8).

As a result of additional observations and analysis, ICRF Extensions 1 and 2 were developed (Fey et al. 2004); the positions of the non-defining sources were improved and new sources were added. The positions of the 212 defining sources were left unchanged.

By 2006, it was recognized that a major update of the ICRF was needed to maintain the accuracy and fixed orientation of the overall frame, and an IAU working group was established to update the list of sources and coordinates. The working group presented a revised and extended list of sources and coordinates. The new list was adopted by the IAU in 2009 as the Second Realization of the International Celestial Reference Frame (ICRF2) (Ma et al. 2009), superseding the original in defining the spatial orientation of the ICRS at S and X bands. The ICRF2 has 295 defining sources, chosen from a solution for the positions of 3414 sources. Only 97 of the defining sources are also defining sources in ICRF1, reflecting the results of the ongoing analysis of source stability and the working group's goal of mitigating source position variations. The positional uncertainties have been reduced considerably and the new list is more evenly distributed across the sky, especially in the south. Typical ICRF2 defining source position errors, all things considered, are not expected to exceed 0.1 milli-arc-seconds. The overall orientation of the axes is estimated to be stable within 0.010 milli-arc-seconds and is consistent with that of ICRF1.

The Frame at Optical Wavelengths

The ICRS is realized at optical wavelengths by stars in the Hipparcos Catalogue of 118218 stars, some as faint as visual magnitude 12 (ESA 1997). Only stars with uncomplicated and well-determined proper motions (e.g., no known binaries) are used for the ICRS realization. This subset, referred to as the Hipparcos Celestial Reference Frame (HCRF), comprises 85% of the stars in the Hipparcos catalog. Hipparcos star coordinates and proper motions are given within the ICRS coordinate system but are listed for epoch J1991.25. (That is, the catalog effectively represents a snapshot of the motion of the stars through space taken on 2 April 1991). At the catalog epoch, Hipparcos uncertainties for stars brighter than 9th magnitude have median values somewhat better than 1 milli-arc-second in position and 1 milli-arc-second/year in proper motion (ESA 1997, Mignard 1997). The overall alignment to the ICRF at that epoch is estimated to be within 0.6 milli-arc-second, with any spurious rotations or distortions less than 0.25 milli-arc-second/year. Projected to epoch 2010, typical position errors for the brighter Hipparcos stars are approximately 20 milli-arc-seconds.

A major reanalysis of the original Hipparcos observations (van Leeuen 2007a, 2007b) has resulted in a new Hipparcos catalog with substantially improved astrometric data. However, the IAU has not taken any action that officially replaces the original Hipparcos catalog as the basis for the HCRF.

Extensions of the ICRS to fainter magnitudes and other wavelength bands are described in the section below titled Data in the ICRS.

Standard Algorithms

At its General Assembly in 2000, the IAU defined a system of space-time coordinates for (1) the solar system, and (2) the Earth, within the framework of General Relativity, by specifying the form of the metric tensors for each and the 4-dimensional space-time transformation between them (IAU 2001). The former is called the Barycentric Celestial Reference System (BCRS), and the latter, the Geocentric Celestial Reference System (GCRS). The BCRS is a "global" reference system in which the positions and motions of bodies outside the immediate environment of the Earth are to be expressed. It is the reference system appropriate for the solution of the equations of motion of solar bodies (that is, the development of solar system ephemerides) and within which the positions and motions of galactic and extra-galactic objects are most simply expressed. It is the system to be used for most positional-astronomy reference data, e.g. star catalogs. The GCRS is a "local" reference system for Earth-based measurements and solution of the equations of motion of bodies in the near-Earth environment, e.g. artificial satellites. Since the IAU definitions of the BCRS and GCRS concern only relativity, they can be thought of as defining two families of reference systems; the IAU 2000 resolutions did not specify an absolute orientation for either; although their relative orientation is described by the transformation between them.
To remedy the situation, in 2006, the IAU passed a resolution (IAU 2008) that specified that the ICRS defines the orientation of the BCRS. Thus, the ICRS and BCRS are closely linked and the two terms are often used interchangeably. A simple way of understanding the connection is that BCRS coordinates are expressed with respect to the ICRS spatial axes and ICRS data are based on the BCRS metric.

Also in 2000 and 2006, the IAU adopted new models for the computation of the Earth's instantaneous orientation within the ICRS. The new models include new algorithms for precession and nutation, a new definition of the celestial pole, and two new reference points in the equatorial plane for measuring the rotational angle of the Earth around its instantaneous axis. These models are described in detail in the IERS Conventions (2010) (Petit & Luzum 2010), in USNO Circular 179 (Kaplan 2005), and in the 2012 edition of the Explanatory Supplement to the Astronomical Almanac (Urban & Seidelmann 2012). These models are important when the instantaneous coordinates of celestial objects are to be expressed with respect to the Equator and Equinox of date, or with respect to a local horizon-based system.

A collection of computer modules in Fortran and C that implement these IAU-recommended algorithms for Earth orientation is the Standards of Fundamental Astronomy (SOFA) library. The collection is managed by an international panel, the SOFA Reviewing Board, which works under the auspices of IAU Division 1 (Fundamental Astronomy). The board solicits code from the astrometric and geodetic community that implements the IAU models. Subroutines/functions are adapted to established coding standards and validated for accuracy before being added to the SOFA collection. The latest version of the U.S. Naval Observatory Vector Astrometry Software (NOVAS), available in Fortran, C, and Python, also implements the IAU models.

The new Earth orientation models are, of course, relevant only to fundamental observations made from the surface of the Earth. Astrometric observations taken from space platforms, or those that are differential in nature (based on reference objects that are all within a small field), are not affected by these models. However, there are other effects that must be taken into account in analyzing astrometric observations-e.g., proper motion, parallax, aberration, and gravitational light-bending-and algorithms for these may be found in Volumes 1 and 3 of the Hipparcos Catalogue documentation ESA (1997) and in the 2012 edition of the Explanatory Supplement to the Astronomical Almanac (Urban & Seidelmann 2012). For analysis of very high accuracy observations from space, see the development by Klioner (2003).

Finally, IAU-recommended models for the rotation of the planets, satellites, and asteroids, compiled by the IAU Working Group on Cartographic Coordinates and Rotational Elements, are given with respect to the ICRS (Archinal, et al. 2011).

Relationship to Other Systems

The orientation of the ICRS axes is consistent with the Equator and Equinox of J2000.0 represented by the FK5, within the errors of the latter. Since, at J2000.0, the errors of the FK5 are significantly worse than those of Hipparcos, the ICRS can be considered to be a refinement of the FK5 system at (or near) that epoch.

The ICRS can also be considered to be a good approximation (at least as good as the FK5) to the conventionally defined dynamical Equator and Equinox of J2000.0 (Feissel & Mignard 1998). In fact, the equator is well determined fundamentally from the VLBI observations that are the basis for the entire ICRS, and the ICRS pole is within 20 milli-arc-seconds of the dynamical pole. As previously mentioned, the zero point of VLBI-derived right ascensions is arbitrary, but traditionally has been set by assigning to the right ascension of source 3C 273B a value derived from lunar occultation timings - the Moon's ephemeris thus providing an indirect link to the dynamical equinox. The ICRS origin of right ascension was made to be consistent with that in a group of VLBI catalogs previously used by the IERS, aligned in this way. The difference between the ICRS origin of right ascension and the dynamical equinox has been independently measured by two groups that used different definitions of the equinox, but in both cases the difference found was less than 0.1 arcsecond.

Because of its consistency with previous reference systems, implementation of the ICRS will be transparent to any applications with accuracy requirements that are not more stringent than about 0.1 arc-seconds. That is, for applications of this accuracy-which is good enough, for example, for telescope pointing, the distinctions between the ICRS, FK5, and dynamical Equator and Equinox of J2000.0 are not significant. However, as mentioned above, implementation of the new IAU Earth orientation models (precession and nutation) is needed to express most accurately (and to avoid systematic errors in) the apparent positions of celestial objects with respect to the Equator and Equinox of date, regardless of which catalog or ephemeris is used for the source data.

For a concise review of the ICRS adoption and its implications, see the paper by Feissel & Mignard (1998).

Data in the ICRS

Although the ICRF2 and HCRF are its basic radio and optical realizations, the ICRS is gradually being extended to fainter magnitudes and other wavelengths. Thus, an increasing amount of fundamental astronomical data is being brought within the new system. A number of projects to this end have been completed and more are in progress.

As described above, the ICRF2 consists of the adopted positions of 3414 extra-galactic radio sources, less than a tenth of which are defining sources. Because all of the observational data were part of a common catalog solution, the adopted coordinates of all the sources are in the ICRS. The non-defining sources tend to have positional uncertainties that are larger than those of the defining sources. Many of the non-defining sources are part of the VLBA Calibrator Survey (described below) and have a very limited observational base - 1966 of them were observed in only one session. Thus their long-term stability has not been evaluated.

The VLBA Calibrator Survey is a list of radio sources, with positions in the ICRS, to be used as calibrators for the Very Long Baseline Array and the Very Large Array. The original list was prepared by Beasley et al. (2002); the list has been extended several times and the current version is known as VCS6 (Petrov et al. 2008). The ICRS is also being established at higher radio frequencies (8, 24, 32, and 43 GHz); see, for example, Jacobs, et al. (2005), Jacobs, et al. (2008), and Lanyi, et al. (2010).

In the optical regime, the Tycho-2 Catalogue (Høg et. al. 2000) combines a re-analysis of the Hipparcos star mapper observations with data from 144 earlier ground-based star catalogs. The ground-based catalogs include the Astrographic Catalogue (AC), a large photographic project carried out near the beginning of the 20th century involving 20 observatories worldwide. Tycho-2 contains 2539913 stars, and combines the accuracy of the recent Tycho position measurements with proper motions derived from a time baseline of almost a century. Proper motion uncertainties are 1-3 milli-arc-seconds/year. The epoch J2000.0 Tycho-2 positions of stars brighter than 9th magnitude are typically uncertain by 20 milli-arc-seconds. However, the positional accuracy degrades quite rapidly for magnitudes fainter than 9, so that 12th magnitude stars generally have a median J2000.0 position error exceeding 100 milli-arc-seconds.

Also in the optical band, the U.S. Naval Observatory CCD Astrograph Catalog (UCAC) provides ICRS-compatible positions and proper motions for 100 million stars over the entire sky as faint as red magnitude 16. See Zacharias (2010) for information on the third release of UCAC data; the fourth and final version is anticipated in 2012. The accuracy of the UCAC4 coordinates near epoch 2000 is estimated to be in the 15-100 milli-arc-second range, depending on magnitude. Proper motion errors are about 1-3 milli-arc-seconds/year for stars to 12th magnitude, and up to 10 milli-arc-seconds/year for fainter stars to 16th magnitude. Observations have begun for a successor catalog, URAT, which will go deeper, to red magnitude 17.5, and will be tied directly to the ICRF2 using the optical counterparts of some of the radio sources defining that frame.

The Large Quasar Reference Frame (LQRF) (Andrei, et al. 2009) is another representation of the ICRS at faint optical magnitudes. It contains the coordinates of 100,165 quasars, well distributed around the sky, accurate to about 100 milli-arc-seconds.

The ICRS has been extended to the near infrared through the Two Micron All Sky Survey (2MASS) (Cutri et al. 2003, Zacharias et al. 2005). This ground-based program provided positions for 471 million point sources, most of which are stars, observed in the J, H, and Ks infrared bands. 2MASS was a single epoch survey without proper motions; positions are listed for J2000.0, which is within the 4-year span of observations. Astrometric accuracy is around 80 milli-arc-seconds in the Ks magnitude range 9-14, with larger errors at both brighter and fainter magnitudes.

The Jet Propulsion Laboratory DE405/LE405 planetary and lunar ephemerides (usually just referred to as DE405) have been aligned to the ICRS (Standish 1998). These ephemerides provide the positions and velocities of the eight planets, Pluto, and the Moon with respect to the solar system barycenter, in rectangular coordinates. The data are represented in Chebyshev series form and Fortran subroutines are provided to read and evaluate the series for any date and time. DE405 spans the years 1600 to 2200; a long version, DE406, spans the years -3000 to +3000 with lower precision. More recent ephemerides from JPL, such as DE421, are also aligned to the ICRS, as are fundamental planetary ephemerides from the Institute of Applied Astronomy (IAA) in Russia and the Institut de Mécanique Céleste et de Calcul des Éphémérides (IMCCE) in France. For a review and comparison of the JPL, IAA, and IMCCE ephemerides, see the papers from Session 2 of the Journées 2010 conference proceedings (Capitaine 2011).

The tabulations in The Astronomical Almanac have been based on ICRS-compatible data sources, including the JPL DE405 planetary and lunar ephemerides, since the 2003 edition. The almanac is prepared using the IAU-recommended algorithms for Earth orientation.

Authorizing IAU Resolutions

The construction and implementation of the ICRS was authorized and supported by the IAU. Resolution B2, passed by the 23rd General Assembly of the IAU in August 1997 (IAU 1999), states that:

• from 1 January 1998, the IAU celestial reference system shall be the International Celestial Reference System (ICRS) as specified in the 1991 IAU Resolution on reference frames and as defined by the International Earth Rotation Service (IERS);
• the corresponding fundamental reference frame shall be the International Celestial Reference Frame (ICRF) constructed by the IAU Working Group on Reference Frames;
• the Hipparcos Catalogue shall be the primary realization of the ICRS at optical wavelengths;
• the IERS should take appropriate measures, in conjunction with the IAU Working Group on Reference Frames, to maintain the ICRF and its ties to the reference frames at other wavelengths.

The "1991 IAU Resolution on reference frames" referred to above was Resolution A4 passed by the 21st IAU General Assembly (IAU 1992). It recommended that "the space coordinate grids with origins at the solar system barycentre and at the centre of mass of the Earth show no global rotation with respect to a set of distant extra-galactic objects" and that "the principal plane of the new conventional reference system be as near as possible to the mean equator of J2000.0 and that the origin in this principal plane be as near as possible to the dynamical equinox of J2000.0." It also recommended that an IAU working group establish a list of extra-galactic radio sources that would be "candidates for primary sources defining the new conventional reference frame." Thus, the ICRS as established in 1997 was based on specifications defined by the IAU in 1991.

At the subsequent IAU General Assembly in 2000, Resolution B1.2 (IAU 2001) restricted the number of Hipparcos stars that would be considered part of the optical realization of the ICRS. The relevant part of this resolution states that:

• Resolution B2 of the XXIIIrd IAU General Assembly (1997) be amended by excluding from the optical realization of the ICRS all stars flagged C, G, O, V and X in the Hipparcos Catalogue;
• this modified Hipparcos frame be labelled the Hipparcos Celestial Reference Frame (HCRF).

Effectively, this change eliminated about 15% of the stars in the Hipparcos catalog, leaving those with well determined linear proper motions. The flags referred to are given in Hipparcos field H59.

Resolutions B1.3. B1.4, B1.5 of the 2000 General Assembly defined the Barycentric Celestial Reference System (BCRS), the Geocentric Celestial Reference System (GCRS), the transformation between them, and the time scales appropriate for each system. Resolutions B1.6, B1.7, and B1.8 of the same General Assembly defined the IAU 2000A precession-nutation model, the celestial pole, points on the celestial and terrestrial equators from which the rotational angle of the Earth is measured, and the expression for the Earth rotation angle as a function of Universal Time (UT1).

At the IAU General Assembly in 2006, Resolution 2 (IAU 2008) completed the definition of the Barycentric Celestial Reference System (BCRS) with the words:
"For all practical applications, unless otherwise stated, the BCRS is assumed to be oriented according to the ICRS axes".

So the fundamental celestial reference system is actually defined by both the BCRS (relativistic metric) and ICRS (orientation). Texts of all IAU resolutions, listed by year of the General Assembly at which they were adopted, can be found at the IAU web site. Extended explanations of the resolutions mentioned here, as well as formulas for their practical implementation, can be found in USNO Circular 179 (Kaplan 2005).

References

Andrei, A. H., Souchay, J., Zacharias, N., Smart, R. L., Vieira Martins, R., da Silva Neto, D. N., Camargo, J. I. B., Assafin, M., Barache, C., Bouquillon, S. Penna, J. L., & Taris, F. (2009): "The Large Quasar Reference Frame (LQRF). An Optical Representation of the ICRS", Astronomy and Astrophysics, Vol. 505, pp. 385-404.

Archinal, B. A., A'Hearn, M. F., Bowell, E., Conrad, A., Consolmagno, G. J., Courtin, R., Fukushima, T., Hestroffer, D., Hilton, J. L., Krasinsky, G. A., and Neumann, G., Oberst, J., Seidelmann, P. K., Stooke, P., Tholen, D. J., Thomas, P. C., & Williams, I. P. (2011): "Report of the IAU Working Group on Cartographic Coordinates and Rotational Elements: 2009", Celestial Mechanics and Dynamical Astronomy, Vol. 109, pp. 101-135.

Beasley, A. J., Gordon, D., Peck, A. B., Petrov, L., MacMillan, D. S., Fomalont, E. B., & Ma, C. (2002): "The VLBA Calibrator Survey-VCS1", Astrophysical Journal Supplement Series, Vol. 141, pp. 13-21.

Capitaine, N., ed. (2011): Systèmes de Référence Spatio-Temporels, Proceedings of the Journées 2010 (Paris: Observatoire de Paris).

Cutri, R. M., Skrutskie, M. F., Van Dyk, S., Beichman, C. A., Carpenter, J. M., Chester, T., Cambresy, L., Evans, T., Fowler, J., Gizis, J., Howard, E., Huchra, J., Jarrett, T., Kopan, E. L., Kirkpatrick, J. D., Light, R. M., Marsh, K. A., McCallon, H., Schneider, S., Stiening, R., Sykes, M., Weinberg, M., Wheaton, W. A., Wheelock, S., & Zacharias, N. (2003): 2MASS All-Sky Catalog of Point Sources, (Pasadena: IPAC/California Institute of Technology)

ESA (1997): The Hipparcos and Tycho Catalogues, European Space Agency pub. SP-1200 (17 volumes).

Feissel, M., & Mignard, F. (1998): "The Adoption of ICRS on 1 January 1998: Meaning and Consequences", Astronomy & Astrophysics, Vol. 331, pp. L33-L36.

Fey, A. L., Ma, C., Arias, E. F., Charlot, P., Feissel-Vernier, M., Gontier, A. M., Jacobs, C. S., Li, J., & MacMillan, D. S. (2004): "The Second Extension of the International Celestial Reference Frame: ICRF-EXT.1", Astronomical Journal, Vol. 127, pp. 3587-3608.

Fricke, W., Schwan, H., Lederle, T., Bastian, U., Bien, R., Burkhardt, G., Du Mont, B., Hering, R., Jahrling, R., Jahreiss, H., Roser, S., Schwerdtfeger, H.-M., & Walter, H. G. (1988): Fifth Fundamental Catalogue (FK5), Part I, The Basic Fundamental Stars. Veroffentlichungen Astronomisches Rechen-Institut, Heidelberg, No. 32.

Høg, E., Fabricius, C., Makarov, V. V., Urban, S., Corbin, T., Wycoff, G., Bastian, U., Schwekendiek, P., & Wicenec, A. (2000): "The Tycho-2 Catalogue of the 2.5 Million Brightest Stars", Astronomy & Astrophysics, Vol. 355, pp. L27-L30.

Hughes, J. A., Smith, C. A., & Kaplan, G. H., eds. (1991): Reference Systems, Proceedings of IAU Colloquium 127 (Washington: USNO).

IAU (1992): Proceedings of the Twenty-First General Assembly, Buenos Aires 1991, ed. J. Bergeron, Transactions of the IAU, Vol. XXI-B (Dordrecht: Kluwer), pp. 30-78.

IAU (1996): Proceedings of the Twenty-Second General Assembly, The Hague 1994, ed. I. Appenzeller, Transactions of the IAU, Vol. XXII-B (Dordrecht: Kluwer), pp. 24-60.

IAU (1999): Proceedings of the Twenty-Third General Assembly, Kyoto 1997, ed. J. Andersen, Transactions of the IAU, Vol. XXIII-B (Dordrecht: Kluwer), pp. 31-51.

IAU (2001): Proceedings of the Twenty-Fourth General Assembly, Manchester 2000, ed. H. Rickman, Transactions of the IAU, Vol. XXIV-B (SanFrancisco: ASP), pp. 34-59.

IAU (2008): Proceedings of the Twenty-Sixth General Assembly, Prague 2006, ed. K. A. van der Hucht, Transactions of the IAU, Vol. XXVI-B (Cambridge: University Press), pp. 34-47.

IAU (2010): Proceedings of the Twenty-Seventh General Assembly, Rio de Janeiro 2009, ed. I. F. Corbett, Transactions of the IAU, Vol. XXVII-B (Cambridge: University Press), pp. 55-70.

Jacobs, C. S., Lanyi, G. E., Naudet, C. J., Sovers, O. J., Zhang, L. D., Charlot, P., Gordon, D. & Ma, C. (2005): "Extending the ICRF to Higher Radio Frequencies: Initial Global Astrometric Results," in The International Celestial Reference System: Maintenance and Future Realizations, Proceedings of IAU General Assembly XXV, Joint Discussion 16, July 2003, ed. R. Gaume, D. D. McCarthy, & J. Souchay (Washington: USNO), pp. 36-43.

Jacobs, C. S. & Sovers, O. J. (2008): "Extending the ICRF above S/X-Band: X/Ka-Band Global Astrometric Results", in Measuring the Future, Proceedings of the Fifth IVS General Meeting, ed. A. Finkelstein & D. Behrend (St. Petersburg: Nauka), pp. 284-288.

Kaplan, G. H., ed. (1982): The IAU Resolutions on Astronomical Constants, Time Scales, and the Fundamental Reference Frame, U.S. Naval Observatory Circular No. 163.

Kaplan, G. H. (2005): The IAU Resolutions on Astronomical Reference Systems, Time Scales, and Earth Rotation Models: Explanation and Implementation, U.S. Naval Observatory Circular No. 179.

Klioner, S. A. (2003): "A Practical Relativistic Model for Microarcsecond Astrometry in Space", Astronomical Journal, Vol. 125, pp. 1580-1597.

Lanyi, G. E., Boboltz, D. A., Charlot, P., Fey, A. L., Fomalont, E. B., Geldzahler, B. J., Gordon, D., Jacobs, C. S., Ma, C., Naudet, C. J., Romney, J. D., Sovers, O. J. & Zhang, L. D. (2010): "The Celestial Reference Frame at 24 and 43 GHz. I. Astrometry", Astronomical Journal, Vol. 139, pp. 1695-1712.

Lieske, J. H., & Abalakin, V. K., eds. (1990): Inertial Coordinate System on the Sky, Proceedings of IAU Symposium 141 (Dordrecht: Kluwer).

Ma, C., & Feissel, M., eds. (1997): Definition and Realization of the International Celestial Reference System by VLBI Astrometry of extra-galactic Objects, IERS Technical Note No. 23, International Earth Rotation and Reference System Service (Paris: Observatoire de Paris).

Ma, C., Arias, E. F., Eubanks, T. M., Fey, A. L., Gontier, A.-M., Jacobs, C. S., Sovers, O. J., Archinal, B. A., & Charlot, P. (1998): "The International Celestial Reference Frame as Realized by Very Long Baseline Interferometry", Astronomical Journal Vol. 116, pp. 516-546.

Ma, C., Arias, E. F., Bianco, G., Boboltz, D. A., Bolotin, S. L., Charlot, P., Engelhardt, G., Fey, A. L., Gaume, R. A., Gontier, A.-M., Heinkelmann, R., Jacobs, C. S., Kurdubov, S., Lambert, S. B., Malkin, Z. M., Nothnagel, A., Petrov, L., Skurikhina, E., Sokolova, J. R., Souchay, J., Sovers, O. J., Tesmer, V., Titov, O. A., Wang, G., Zharov, V. E., Barache, C., Boeckmann, S., Collioud, A., Gipson, J. M., Gordon, D., Lytvyn, S. O., MacMillan, D. S., & Ojha, R. (2009): The Second Realization of the International Celestial Reference Frame by Very Long Baseline Interferometry, IERS Technical Note No. 35, International Earth Rotation and Reference System Service (Frankfurt am Main: Verlag des Bundsesamts fur Kartographie und Geodasie).

Mignard, F. (1997): "Astrometric Properties of the Hipparcos Catalogue", in Proceedings of the ESA Symposium "Hipparcos-Venice '97", European Space Agency pub. SP-402, pp. 5-10.

Petit, G. & Luzum, B., eds. (2010): IERS Conventions (2010), IERS Technical Note No. 36, International Earth Rotation and Reference System Service (Frankfurt am Main: Verlag des Bundsesamts fur Kartographie und Geodasie).

Petrov, L., Kovalev, Y. Y., Fomalont, E. B., & Gordon, D. (2008): "The Sixth VLBA Calibrator Survey: VCS6", Astronomical Journal, Vol. 136, pp. 580-585.

Standish, E. M. (1998): "JPL Planetary and Lunar Ephemerides, DE405/LE405", Jet Propulsion Laboratory Interoffice Memorandum IOM 312.F-98-048.

Urban, S. E. & Seidelmann, P. K., eds. (2012): Explanatory Supplement to the Astronomical Almanac (Mill Valley, CA: University Science Books).

van Leeuwen, F., ed. (2007a): "Hipparcos, the New Reduction of the Raw Data", Astrophysics and Space Science Library, Vol. 350.

Van Leeuwen, F. (2007b): "Validation of the New Hipparcos Reduction", Astronomy and Astrophysics, Vol. 474, pp. 653-664.

Zacharias, N., McCallon, H. L., Kopan, E., & Cutri, R. M. (2005): "Extending the ICRF into the Infrared: 2MASS-UCAC astrometry," in The International Celestial Reference System: Maintenance and Future Realizations, Proceedings of IAU General Assembly XXV, Joint Discussion 16, July 2003, ed. R. Gaume, D. D. McCarthy, & J. Souchay (Washington: USNO), pp. 52-59.

Zacharias, N., Finch, C., Girard, T., Hambly, N., Wycoff, G., Zacharias, M. I., Castillo, D., Corbin, T., DiVittorio, M., Dutta, S., Gaume, R., Gauss, S., Germain, M., Hall, D., Hartkopf, W., Hsu, D., Holdenried, E., Makarov, V., Martinez, M., Mason, B., Monet, D., Rafferty, T., Rhodes, A., Siemers, T., Smith, D., Tilleman, T., Urban, S., Wieder, G., Winter, L. & Young, A. (2010): "The Third US Naval Observatory CCD Astrograph Catalog (UCAC3)", Astronomical Journal, Vol. 139, pp. 2184-2199.