Ageton Tables

Ageton's Tables for Sight Reduction

Sight Reduction is the process of solving the Navigational Triangle for an Assumed Position and the position of an observed Celestial Body in order to obtain a Line-of-Position. In the beginning of the 20th century Arthur A. Ageton developed a method of solving the oblique navigational triangle by dividing it into two right-angled triangles, which can be solved with less complex trigonometric operations.

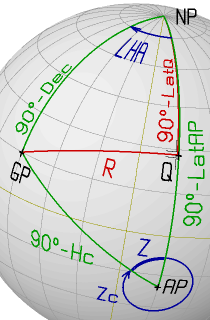
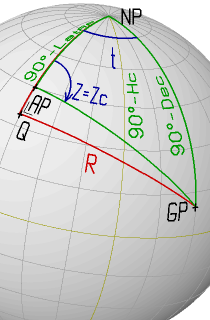
The oblique navigational triangle between the Geographical Point (GP) of the observed celestial body, the Geographical North Pole (NP) and the Assumed Position (AP) of the observer is divided into two right-angled triangles by a great-circle segment "R" starting at GP and intersecting the Meridian through AP at a right angle. This defines a new triangle side "R" and a new triangle vertex point "Q". This point has the same Longitude as the Assumed Position and a Latitude "LatQ". Notice, that except if GP is on the Equator, the Latitude of "Q" is different from the Latitude of GP.

By solving the two the right-angled triangles, the values for the Altitude (Hc) and Azimuth (Zc) can be obtained with less complex trigonometric calculations at the price of a larger number of operations. The main advantage of this method is that only two simple trigonometric functions are required, which can be tabulated in a much denser form compared to the tables needed for solving the oblique navigational triangle directly (as e.g. in the "H.O. 229" Tables).

Solving the divided Navigational Triangle

For the sight-reduction problem, the Navigational Triangle has be solved to obtain the calculated values for Altitude (Hc) and Azimuth (Zc) for an Assumed Position with coordinates: assumed Latitude (LatAP) and assumed Longitude (LonAP) and the celestial coordinates of the observed body: Declination (Dec) and Greenwich Hour Angle (GHA).
The Method of Ageton includes two additional - intermediate - values: the Latitude of the vertex "Q" (LatQ) and the length of the intermediate side "R" (see picture at the top of this section).

Altitude (Hc) and Azimuth (Zc) may be obtained through the following 7 steps:

 1. LHA  = GHA + LonAP

Solve the sides of the first right-angled triangle (Law of Sines and Law of Cosines for Sides):

 2. sin(R)    = sin(LHA)*cos(Dec)
 3. sin(LatQ) = sin(Dec)/cos(R)

Solve the second right-angled triangle for Hc and Zc (Law of Sines and Law of Cosines for Sides):

 4. dLat      = LatAP - LatQ
 5. sin(Hc)   = cos(R)*cos(dLat)
 6. sin(Z)    = sin(R)/cos(Hc)

If the North Pole is systematically used as reference pole (even if the elevated pole is the South Pole), the true Azimuth Zc is obtained from Z through the following rule:

 7. if LHA < 180°  then  Zc = Z
    if LHA > 180°  then  Zc = 360° - Z

Ageton reformulated the above equations using the Secant (sec(x) = 1/cos(x) ) and Cosecant ( csc(x) = 1/sin(x) ) functions. Additionally he introduced logarithms to change multiplication and division operations into much simpler addition and subtraction operations. The steps for solving the divided navigational triangle can then be reformulated as:

 2. csc(R)    = csc(LHA)*sec(Dec)
 3. csc(LatQ) = csc(Dec)/sec(R)

 5. csc(Hc)   = sec(R)*sec(dLat)
 6. csc(Z)    = csc(R)/sec(Hc)

Introducing the logarithmic functions A(x)=log₁₀(csc(x)) and B(x)=log₁₀(sec(x)) this becomes:

 2. A(R)    = A(LHA) + B(Dec)
 3. A(LatQ) = A(Dec) - B(R)

 5. A(Hc)   = B(R)   + B(LatQ-LatAP)
 6. A(Z)    = A(R)   - B(Hc)

With the values A(x) and B(x) available (e.g. as precompiled tables) a sight can be reduced by a series of additions, subtractions and table look-ups.

Remarks:
1. Since the Ageton Tables are available only for x in the range [0° < x < 180°], the Meridian Angle (t) must be used instead of the Local Hour Angle (LHA) according to:

 t = -LHA        if LHA < 180°
 t = 360° - LHA  if LHA > 180°

2. Since the logarithmic functions A(x) and B(x) cannot preserve the correct sign of the argument x, the sign of each angle obtained by backward table look-up must be derived from the actual geometry of the Navigational Triangle. Therefore, it is highly recommended to sketch the spherical triangles involved while solving them for the required values.

Purpose and Scope

The Ageton Tables can be used to solve right-angled spherical triangles, as part of the sight-reduction process or other navigational problems based on the general navigational triangle.

The Ageton Tables, first published by the Hydrographic Office as HO211 in 1931, contain the tabulated values of the the Secant (sec(x) = 1/cos(x) ) and Cosecant ( csc(x) = 1/sin(x) ) functions in the following form:

A(x) = 100 000 * log₁₀( 1/sin(x) )
B(x) = 100 000 * log₁₀( 1/cos(x) )

The multiplication factor 100 000 is used to tabulate the functions A(x) and B(x) as integer values thus simplifying the addition and subtraction of these values. In the original tables, the functions A(x)/B(x) were recorded with an angle increment of 0.5' for a range [0° < x < 180°]. Notice that the function A(x) is undefined for x=0° and x=180°, whereas the function B(x) is undefined for x=90°.
The Ageton Method may give unreliable results if one of the angles involved in the Sight Reduction process is close to 0°, 90° or 180°. In order to obtain the best possible accuracy, the Ageton Tables should be used with linear interpolation in both directions: forward (from x to A(x)/B(x)) and backward (from A(x)/B(x) to x).

Tables

Arrangement

In the tables available here, each page contains the values of A(x) and B(x) for an interval of one degree with a 0.2' angle increment. Since the logarithmic tables do not consider the sign of the Cosecant and Secant functions, each table entry for an angle x can also be used for it's supplementary value 180°-x. This value is printed in the bottom line of the table. The fractional value of the argument is obtained from the corresponding column (deca-minutes) and row (minutes). As indicated by the table background colour of the interactive tables, use the top/left minute labels for the degree value in the top row and use the bottom/right minute labels for the degree value at the bottom row.

Interactive Tables

Table

With the links on the left, a specific page of the Ageton Tables can be generated. The pages are "numbered" from 0° to 89°. This number can be entered in the "Angle" field to generate the corresponding page of the Tables.
In order to obtain reliable results, the B(x) values should not be used for angles lower than 3° whereas the A(x) values should not be used for angles higher than 87°.

Precompiled Tables

The complete Ageton Tables are also available as compiled tables in PDF format. The same tables are also available in a booklet format. In order to obtain the booklet, print this file double-sided, then fold each page and glue the folded edges of all pages together. In the tables, some ranges for A(x) and B(x) have been shaded grey. To obtain reliable results, these ranges should not be used in the calculation process for sight reduction.

PDF files can be viewed and printed with free available tools such as Evince, Xpdf or Acrobat Reader.

Note on accuracy

An extensive error analysis was performed with the following conditions:

parameter ranges:
- [-90° < t < +90°]
- [-70° < Latitude (LatAP) < +70° ]
- [-30° < Declination (Dec) < +30° ]
parameter combinations yielding an Altitude of less than 6° are discarded
sights for which the the grey shaded regions of the tables have to be used are discarded (this is the case for about 8% of the valid combinations with an Altitude above 6°).

For all parameter combinations in the above mentioned ranges (with a resolution of 0.05°) the results of the sight reduction obtained with the table-based Ageton method were compared to the results obtained by solving directly the trigonometric equations of the navigational triangle. This comparison results in the following statistics on the evaluated error for the Altitude "Hc":

the maximum error is ±2.1' (minutes of arc)
the mean error over all valid combinations is 0.1'
90.0% of the valid combinations have an absolute error lower than 0.2'
99.0% of the valid combinations have an absolute error lower than 0.5'
99.9% of the valid combinations have an absolute error lower than 0.8'
0.0004% of the valid combinations have an absolute error larger than 1.0'

The Sight Reductions performed with the tables were done using simple linear interpolation on the recorded table values. The accuracy can be increased by using a higher multiplication factor (e.g. if a factor 1000000 is used instead of 100000, the maximum error is ±1.2')
The maximum error on the calculated Azimuth "Zc" for the investigated parameter space is lower than 20' (0.3°), which is accurate enough to obtain a reliable Azimuth Line at the Assumed Position.

Calculation Scheme

The following scheme can be applied for sight reduction using the above presented Tables. Close attention should be paid to the remarks and instructions at the lower part of the form!

                                                                              Remarks     
     AP:  LatAP  =  ±__°__'_ (N/S)           GP:    Dec =  ±__°__'_ (N/S)       (0)
          LonAP  = ±___°__'_ (E/W)                  GHA =  ___°__'_ 


     1.   LHA    = GHA + LonAP   =  ___°__'_
            t    =     - LHA     = ±___°__'_         if( LHA < 180°)            (1)
            t    = 360°- LHA     = ±___°__'_         if( LHA > 180°)
          A(t)   = ________

     2.   A(Dec) = ________                      B(Dec) = ________

     3.   A(R)   = A(t) + B(Dec) = ________ + ________  = ________
            R    =  __°__'_                        B(R) = ________

     4.   A(LatQ)= A(Dec) - B(R) = ________ - ________  = ________
            LatQ = ±__°__'_ (N/S)                                              (4)

     5.     dLat = LatAP - LatQ  = ±__°__'_ - ±__°__'_  = ±___°__'_            (5)
          B(dLat)= ________

     6.    A(Hc) = B(R) + B(dLat) = ________ + ________  = ________
             Hc  =  __°__'_                        B(Hc) = ________

     7.    A(Z)  = A(R) - B(Hc)   = ________ - ________  = ________
             Z   =  __°__'_                                                    (7)

     8.      Zc  = ___°__'_                                                    (8)           



  Remarks and Instructions
  (0)  Use the appropriate signs for Latitude, Longitude and Declination: 
       positive for N and E, negative for S and W. 
 
  (1)  The meridian angle "t" is calculated from "LHA" according to the following rule:
       if LHA < 180°   t =      - LHA         (GP is WEST of AP)
       if LHA > 180°   t = 360° - LHA         (GP is EAST of AP)
 
  (4)  The sign of the Latitude of "Q" (N/S) depends on the values of "t" and "Dec": 
       if |t| < 90°   LatQ has the     same sign as Dec
       if |t| > 90°   LatQ has the contrary sign of Dec
       Where |t| is the absolute value of "t"

  (5)  The value of "dLat" must be calculated taking the correct signs for "LatAP" and
       "LatQ" into account. The resulting sign of "dLat" should be recorded correcly
       (see remark 7).

  (7)  Select one out of four cases, depending on the value of "|t|" and the sign of 
       "dLat" to determine how to select the value of "Z" from the Tables:
         |t|     |       |t| < 90°       |       |t| > 90°       |
         dLat    |      -    |     +     |     -     |     +     |
          Z      |   < 90°   |  > 90°    |   > 90°   |   < 90°   |
       if Z < 90° select Z from the    top line - left  column of the Table
       if Z > 90° select Z from the bottom line - right column of the Table

  (8)  The true Azimuth "Zc" is obtained from "Z" depending on the sign of "t":
       if t > 0   Zc = Z            (GP is East of AP)
       if t < 0   Zc = 360° - Z     (GP is West of AP)

This form is also available as printer ready pdf file: worksheet for Sight Reduction according to Ageton.

Examples

In the following section, some examples of Sight Reduction using the Ageton Tables are elaborated. The examples cover most combinations of Assumed Position (N/S), Declination (N/S) of the celestial body and possible Meridian Angles.

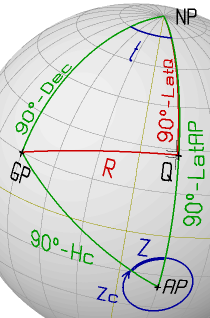
Example 1

AP: LatAP= -20° 00'0 (S)         GP: Dec= +15° 00'0 (N)
    LonAP= +15° 00'0 (E)             GHA= 045° 00'0 (W)


 1. t = GHA+LonAP = 60° 00.0'          A(t)=  6247

 2. A(R)   = A(t) + B(Dec) =  6247 +  1506 =  7753  
      R    =  56° 46'4                 B(R)= 26126

 3. A(LatQ)= A(Dec) - B(R) = 58700 - 26126 = 32574
      LatQ = +28° 11'3       (sign determined from topology)

    dLat   = LatQ-LatAP = 48° 11'3  B(dlat)= 26126

 4. A(Hc)  = B(R) + B(dLat)= 26126 + 17609 = 43735
      Hc   =  21° 25'6               B(Hc) =  3111

 5. A(Z)   = A(R) - B(Hc)  =  7753 -  3111 =  4642
      Z    =  63° 58'6       (value selected from topology)              
      Zc   = 296° 01'4       (rule determined from topology)

The same values are obtained when solving the oblique triangle directly with an electronic calculator: Hc = 21° 25'6 and Zc = 296° 01'4.

Example 2

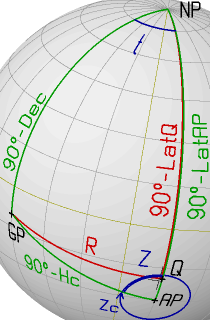AP: LatAP= -30° 00'0 (S)         GP: Dec= -10° 00'0 (S)
    LonAP= +15° 00'0 (E)             GHA= 045° 00'0 (W)


 1. t = GHA+LonAP = 60° 00.0'          A(t)=  6247

 2. A(R)   = A(t) + B(Dec) =  6247 +   665 =  6912  
      R    =  58° 31'5                 B(R)= 28222

 3. A(LatQ)= A(Dec) - B(R) = 76033 - 28222 = 47811
      LatQ = -19° 25'5       (sign determined from topology)

    dLat   = LatQ-LatAP = 10° 34'5  B(dlat)=   744

 4. A(Hc)  = B(R) + B(dLat)= 28222 +   744 = 28966
      Hc   =  30° 52'9               B(Hc) =  6639

 5. A(Z)   = A(R) - B(Hc)  =  6912 -  6639 =   273
      Z    =  83° 35'0       (value selected from topology)  
      Zc   = 276° 25'0       (rule determined from topology)

Slightly different values are obtained when solving the oblique triangle directly with an electronic calculator: Hc = 30° 52'8 and Zc = 276° 24'6.

Example 3

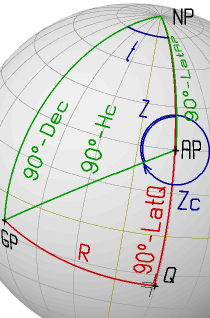AP: LatAP= +30° 00'0 (N)         GP: Dec= -10° 00'0 (S)
    LonAP= +15° 00'0 (E)             GHA= 045° 00'0 (W)


 1. t = GHA+LonAP = 60° 00.0'          A(t)=  6247

 2. A(R)   = A(t) + B(Dec) =  6247 +   665 =  6912  
      R    =  58° 31'5                 B(R)= 28222

 3. A(LatQ)= A(Dec) - B(R) = 76033 - 28222 = 47811
      LatQ = -19° 25'5       (sign determined from topology)

    dLat   = LatAP-LatQ = 49° 25'5  B(dlat)= 18679

 4. A(Hc)  = B(R) + B(dLat)= 28222 + 18679 = 46901
      Hc   =  19° 51'2               B(Hc) =  2661

 5. A(Z)   = A(R) - B(Hc)  =  6912 -  2661 =  4251
      Z    = 114° 56'4       (value selected from topology)  
      Zc   = 245° 03'6       (rule determined from topology)

Slightly different values are obtained when solving the oblique triangle directly with an electronic calculator: Hc = 19° 51'1 and Zc = 245° 03'6.

Example 4

AP: LatAP= +45° 00'0 (N)         GP: Dec= +10° 00'0 (N)
    LonAP= -45° 00'0 (W)             GHA= 330° 00'0 (E)


 1. t = GHA+LonAP = 75° 00.0'          A(t)=  1506

 2. A(R)   = A(t) + B(Dec) =  1506 +   665 =  2171  
      R    =  72° 02'0                 B(R)= 51080

 3. A(LatQ)= A(Dec) - B(R) = 76033 - 51080 = 24953
      LatQ = +34° 15'6       (sign determined from topology)

    dLat   = LatAP-LatQ = 10° 44'4  B(dlat)=   768

 4. A(Hc)  = B(R) + B(dLat)= 51080 +   768 = 51848
      Hc   =  17° 38'5               B(Hc) =  2092

 5. A(Z)   = A(R) - B(Hc)  =  2171 -  2092 =    79
      Z    =  93° 27'3       (value selected from topology)  
      Zc   =  93° 27'3       (rule determined from topology)

Slightly different values are obtained when solving the oblique triangle directly with an electronic calculator: Hc = 17° 38'3 and Zc = 093° 27'3.

Cover << Sail Away << Celestial Navigation << .

last updated: 30-Nov-2008