Geodesy
Geodesy is the science concerned with the exact size and shape of the surface
of the Earth. It also involves the study of variations of the Earth's gravity.
These precise knowledge and measurements were unimportant to early
navigators, because of the relative inaccuracy of their methods. The precision
of today's navigation systems and the global nature of satellite and other
long-range positioning methods demand a more complete understanding of
geodesy.
The Shape of the Earth
The Greek philosophers were the first to theorize that the Earth was round.
However, in their speculation and theorizing, the shape of the Earth ranged
from the flat disc advocated by Homer to Pythagoras' spherical figure -
an idea supported one hundred years later by Aristotles. Pythagoras was
a mathematician and to him the most perfect figure was a sphere. He reasoned
that the gods would create a perfect figure and therefore the Earth was
created to be spherical in shape. Anaximenes, an early Greek scientist,
believed strongly that the Earth was rectangular in shape.
Since the spherical shape was the most widely supported during the Greek
Era, efforts to determine its size followed. Plato determined the circumference
of the Earth to be 400 000 stadia while Archimedes estimated 300 000 stadia.
Plato's figure was a guess and Archimedes' a more conservative approximation.
Meanwhile, in Alexandria (Egypt), a Greek scholar and philosopher, Eratosthenes, set
out to make more explicit measurements.
Eratosthenes born 275 BC in Cyrene - then Greece now in Lybia - studied
at Alexandria and Athens and became director of the Great Library at Alexandria
in 236 BC. Inspired by his readings of the works of Posidonius, Eratosthenes
was the first who tried to experimentally estimate the dimensions of the Earth.
 |
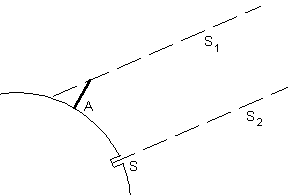
From his readings he had learnt that once a year - on the day
of the summer solstice - the bottom of a well situated in Syene (now Aswan
on the Nile in Upper Egypt) was illuminated by the Sun. However, in Alexandria,
this never happened.
Eratosthenes then set up the following experiment: he assumed that Alexandria
and Syene were on the same Meridian (the difference in longitude is actually around 3°)
and he postulated that the Sun is far enough away from the Earth such that
the sunlight reaches the Earth as parallel beams (an idea that was already
commonly held by ancient Greek mathematicians). |
|
Further he knew from the trading caravans that the distance from Syene
to Alexandria was 5000 stadia. 100 stadia was the distance an average caravan
of camels would travel in one day. Although our idea of the exact value
of the stadium - which was not the same at Athens, Alexandria or Rome -
is fairly vague, it is believed to be around 180 metres. |
|
On the summer solstice day (around the 21th of June)
at local noon, Eratosthenes measured the length of a gnomon (probably he
used an obelisk with a known height) at Alexandria.
The measurement showed that the length of the shadow was 1/8th of the
height of the gnomon, yielding an incident angle of 7.12°.
From this he concluded that the circumference of the Earth must be 360°/7.12°
= 50.6 times the distance Syene-Alexandria.
Eratosthenes had assumed that this distance was 5000 stadia, fixing the
terrestrial circumference to 252800 stadia. Using the consensus value of 180 metres for
one stadium, this corresponds to 45500 km. Today we know, the distance Aswan-Alexandria
is about 840 km, with a resulting circumference of 42400 km. So with this simple experiment
- and some luck, because some errors advantageously cancelled out -
Eratosthenes obtained a reasonable good value for the size of the Earth. |
 |
Ancient Greek philosophers concluded that the Earth could only be a
sphere because that, in their opinion, was the "most perfect" shape. Today
we know that the shape of the Earth is much more complex and consists of
a very complex and irregular topographic surface.
The topographic surface is generally the concern of topographers and hydrographers.
The irregular shape of the topographic surface is simplified in a first
step by defining a geoid. The geoid is a surface along which gravity
is constant and to which the direction of gravity is perpendicular. The
geoid is a surface along which the gravity potential is everywhere equal
and to which the direction of gravity is always perpendicular. The later
is particularly significant because optical instruments containing levelling
devices are commonly used to make geodetic measurements.
The geoid is that surface to which the oceans would conform over the
Earth if free to adjust to the combined effect of the Earth's mass attraction
and the centrifugal force of the Earth's rotation. Uneven distribution
of the Earth's mass makes the geoidal surface irregular. The surface of
the geoid, with some exceptions, tends to rise under mountains and to dip
above ocean basins.
The geoid refers to the actual size and shape of the Earth, but such
an irregular surface has serious limitations as a mathematical Earth model.
For mapping and charting purposes, it is necessary to use a regular
geometric shape which closely approximates the shape of the geoid either
on a local or global scale, and which has a specific mathematical expression.
This "mathematical" model is called the ellipsoid.
Geodetic Systems
Since the Earth is in fact flattened slightly at the poles and bulges somewhat
at the equator, the geometrical figure used in geodesy to most nearly approximate
the shape of the Earth is an ellipsoid of revolution. The ellipsoid of
revolution is the figure which would be obtained by rotating an ellipse
about its shorter axis.
An ellipsoid of revolution is uniquely defined by two parameters. Geodesists,
by convention use the parameters "semi-major axis" and "flattening". The
size of the ellipsoid is determined by the semi-major axis, which will
be the Earth radius at the Equator. The shape is given by the flattening,
which indicates how closely an ellipsoid approaches a perfect spherical
shape. The flattening for the Earth is about 1/300 and the ratio of the
two axis of the ellipsoid is about 299/300.
Since the ellipsoid is used to approximate the irregular surface of
the geoid, an ellipsoid can provide only a good approximation for a part
of the geoidal surface. The ellipsoid that fits best in North America is
different from the ellipsoid that fits best for Europe. Therefore a number
of different reference ellipsoids are used in geodesy and mapping.
The ellipsoids listed below have had utility in geodetic work and many
are still in use. The older ellipsoids are named for the individual who
derived them and the year of development is given. The international ellipsoid
was developed by Hayford in 1910 and adopted by the International Union
of Geospatial Sciences Division (IUGG) which recommended it for international
use.
| Name |
Equatorial Radius |
Flattening |
Used in |
| Krassowsky (1940) |
6,378,245m |
1/298.30 |
Russia |
| International (1924) |
6,378,388m |
1/297.00 |
Europe |
| Clarke (1880) |
6,378,249m |
1/293.46 |
France, Africa |
| Clarke (1866) |
6,378,206m |
1/294.98 |
North America |
| Bessel (1841) |
6,377,397m |
1/299.15 |
Japan |
| Airy (1830) |
6,377,563m |
1/299.32 |
Great Britain |
| Everest (1830) |
6,377,276m |
1/300.80 |
India |
| WGS 66 (1966) |
6,378,145m |
1/298.25 |
USA |
| GRS-67 (1967) |
6,378,160m |
1/298.25 |
Australia,South America |
| WGS-72 (1972) |
6,378,135m |
1/298.26 |
USA |
| GRS-80 (1979) |
6 378 137m |
1/298.26 |
|
| WGS-84 (1984) |
6,378,137m |
1/298.26 |
USA |
At the 1967 meeting of the IUGG held in Lucerne, Switzerland, the ellipsoid
called GRS-67 in the listing was recommended for adoption. The new ellipsoid
was not recommended to replace the International Ellipsoid (1924), but
was advocated for use where a greater degree of accuracy is required. It
became a part of the Geodetic Reference System 1967 which was approved
and adopted at the 1971 meeting of the IUGG held in Moscow. It is used
in Australia for the Australian Geodetic Datum and in South America for
the South American Datum 1969.
The ellipsoid called GRS-80 (Geodetic Reference System 1980) was approved
and adopted at the 1979 meeting of the IUGG held in Canberra, Australia.
The ellipsoids used to define WGS 66 and WGS 72 are discussed in ...
Notice: Referencing geodetic coordinates to the wrong datum can
result in position errors of hundreds of meters!
Global Reference Systems and Reference Frames
An important underlying concept is that definitions of reference systems
are purely definitions and must be "realised" through some defined process.
At the most fundamental level, two types of reference systems are of interest.
The first is the Celestial Reference System (CRS) which is a space fixed
system to which the positions of celestial objects are referred.
The second reference system of relevance is the Conventional Terrestrial
Reference System (CTRS). The International Terrestrial Reference System
(ITRS) is a particular realisation of the CTRS. The ITRS has the following
characteristics:
The origin is at the centre of mass of the whole Earth including the oceans
and atmosphere. The unit of length is the metre.
The orientation of its axes is consistent with that of the Bureau International
de l'Heure (noe IERS) at the beginning of 1984.
Changes in orientation over time are such that there is no residual rotation
with respect to the horizontal movement of the Earth's crust.
The International Earth Rotation Service (IERS)
has been established since 1988 jointly by the International Astronomical
Union (IAU) and the International Union
of Geodesy and Geophysics (IUGG). The
IERS mission is to provide to the worldwide scientific and technical community
reference values for Earth orientation parameters and reference realizations
of internationally accepted celestial and terrestrial reference systems.
The IERS is in charge to realize, use and promote the International
Terrestrial Reference System (ITRS) as defined by the IUGG resolution No
2 adopted in Vienna,1991.
In the geodetic terminology, a reference frame is a set of points with
their coordinates which realize an ideal reference system. The frames produced
by IERS as realizations of ITRS are named International Terrestrial Reference
Frames (ITRF).
Three particularly relevant realisations of the ITRS are the
International Terrestrial Reference Frame (ITRF), WGS84 as used for GPS and PZ90 as used for GLONASS.
WGS-84
WGS-84 is an Earth fixed global reference frame, including an Earth model,
which was established by the US Defense Mapping Agency (now the National
Imaging and Mapping Agency, NIMA). It is defined by a set of primary and
secondary parameters:
the primary parameters define the shape of an Earth ellipsoid, its angular
velocity, and the Earth mass which is included in the ellipsoid reference
the secondary parameters define a detailed gravity model of the Earth.
These additional parameters are needed because WGS-84 is used not only
for defining coordinates in surveying, but, for example, also for determining
the orbits of GPS navigation satellites.
The significance of WGS-84 comes about because GPS receivers rely on
WGS-84. The satellites send their positions in WGS-84 as part of the broadcast
signal recorded by the receivers (the so-called Broadcast Ephemeris) and
all calculations internal to receivers are performed in WGS-84.
From a technical point of view, WGS-84 is a particular realization of
the CTRS (conventional terrestrial reference system). It is established
by the National Imagery and Mapping Agency (NIMA) of the US Department
of Defence. The initial realization of WGS-84 relied on Transit System
observations and was only accurate at the meter level.
Since 1994 (start of GPS Week 730) the use of a revised value of the
gravitation constant along with improved coordinates for the Air Force
and NIMA GPS tracking stations led to the WGS-84 G730 geodetic system.
That realization was shown to be consistent with the ITRF (International
terrestrial reference frame) at the 10 centimetre level.
Further improvements to the tracking station coordinates in 1996 led
to WGS-84 G873. The G873 coordinates were implemented in the GPS Operational
Control Segment on 29 January 1997. Tests have shown WGS-84 G873 to be
coincident with the ITRF94 at a level better than 2cm.
It should also be noted that the ellipsoid used for WGS-84 agrees with
that of the Geodetic Reference System of
1980 (GRS-80) except for a very small difference in the flattening
term. GRS80 is the reference ellipsoid associated with ITRF.
Working with WGS-84
It should be noted that there are only two ways to directly produce
WGS-84 coordinates. The first is by GPS
surveying measurements relative to the US DoDs GPS tracking stations.
However, the GPS data from those DoD
stations is not typically available to civilians. The second way is
by point positioning using a GPS receiver.
However, the accuracy of point positions performed by civilians is
limited by the policy of Selective Availability to
+/- 100m at 95% confidence. Only US DoD or allied military agencies
can perform point positioning with
centimetre to decimetre accuracy.
Civilian surveyors often require WGS-84 coordinates to an accuracy better
than that available from point
positioning. For example, a common requirement for accurate WGS-84
coordinates is to seed the processing of
GPS surveying baselines. However as outlined above, civilians cannot
access WGS-84 directly with high accuracy and must therefore resort to
indirect means to produce WGS-84 compatible coordinates.
One way to obtain more accurate WGS-84 compatible coordinates is to
use local datum coordinates and a published transformation process. In
practice, a transformation process is derived between data sets on both
datum and any errors in those data sets affect the transformation process.
The quasi WGS84 coordinates that result from a transformation process can
be in error in an absolute sense by as much as several metres but are usually
more accurate in a relative sense. Transformation processes in common use
include the three parameter
Molodensky method (or block shift), seven parameter (or similarity)
transformation, multiple regression equations and surface fitting approaches.
The most rigorous way for civilian surveyors to produce WGS84 compatible
coordinates is to perform GPS
surveying measurements relative to control stations with published
ITRF coordinates. That will produce ITRF
coordinates for any new stations. As outlined above, ITRF94 (or later)
coordinates can then be claimed to be
An important mechanism allowing the ITRF to be accessible for geodetic
networks anywhere in the world is the
ability to access precise ephemeris for the GPS satellites and precise
station coordinates from the International
GPS for Geodynamics Service (IGS). The IGS has a global network of
stations with high quality receivers
observing GPS continuously (Zumberger et al 1995).
Given widespread use of GPS, there is a trend for the working geodetic
datum to be consistent with recent ITRF
and therefore with WGS84. This trend was set with the North American
Datum of 1983 as a geocentric datum
using the GRS80 ellipsoid. Recent implementations have taken advantage
of the continued development of the
various ITRF (e.g. for European developments see Seeger, 1994). Australia
is also progressing toward adoption of
an ITRF based geocentric datum by the year 2000 (Manning and Harvey,
1994). In such cases where the modern
geodetic datum is based on a recent ITRF it will be compatible with
WGS84 at the few centimetre level.
|

