Notes on Loxodrome Calculations

In navigation, commonly tracks of constant course (constant heading) are sailed or planned. A track of constant course is a line making the same angle with all meridians and can readily be steered using a compass. Such a line of constant heading is called a rhumb line or loxodrome.

For the navigator, the distance of such rhumb-line tracks is an important piece of information enabling for example to estimate the time-of-arrival at some point ahead or to determine the current average travelling speed.

Except with the graphical chart plotting technique, rhumb-line distances and courses may also be calculated mathematically. This may be useful e.g. for determining the loxodrome distance of long tracks covering more than one chart. Also for determining the loxodrome course and distance of transatlantic journeys this mathematical approach may be useful.

Notice, that in the following calculations, the distance D is assumed to be expressed in degrees. The transformation factor between nautical miles and degrees is:

 1 nautical mile = 1/60 degrees

Furthermore, it is assumed that angles as well as the arguments of the trigonometric functions are expressed in degrees. Consequently, the results of the inverse trigonometric functions will be degrees.

The Loxodrome Equation in the Mercator Projection

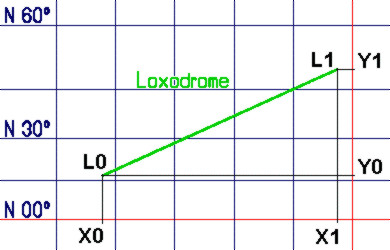
For finding the equation of a loxodrome connecting two arbitrary points on the surface of the Earth, the location of the two points may be transferred onto a Mercator grid. A straight line connecting the two points in the Mercator grid represents the loxodrome and the angle under which this straight line intersects with a vertical line (Meridian) is the true course for this rhumb line.

The Mercator transformation may be described as follows: two arbitrary locations L0 and L1 are specified by their Latitude, Longitude coordinates on the surface of the Earth:

  Location L0: (Lat0, Lon0)
  Location L1: (Lat1, Lon1)

The Mercator transformation maps these points onto a plane (X,Y) Mercator grid:

  Location L0: X0 = Lon0; Y0 = ln( tan(Lat0/2+45°) ) * 57.2958
  Location L1: X1 = Lon1; Y1 = ln( tan(Lat1/2+45°) ) * 57.2958 

The factor "57.2958" is a scaling factor to assure conformality. It is determined by 180°/PI = 57.2958 °/rad. This scaling of the Latitude axis assures that - on the Equator - the distance of one degree of Latitude equals the distance of one degree of Longitude.

A straight line from (X0,Y0) to (X1,Y1) is the Loxodrome, connecting the locations L0 and L1. The general equation of a line connecting two points (x0,y0) and (x1,y1) in a two-dimensional (x,y) space is given by:

  (y -y0) = (x -x0)      or      y = (y1-y0) * (x-x0) + y0
  (y1-y0)   (x1-x0)                  (x1-x0)
 

Applying this for the two points of the loxodrome (X0,Y0) and (X1,Y1), the equation for the loxodrome in the plane Mercator grid is given by:

  Y = (Y1-Y0) * (x-X0) + Y0
      (X1-X0)
 

Filling in the Mercator transformed values (X0,Y0) and (Y1,Y1) for the locations L0 and L1, yields the equation of the Loxodrome in the Mercator plane:

  Y = 57.2958 * ( [ ln(tan(Lat1/2+45°)/tan(Lat0/2+45°)) ] + ln(tan(Lat0/2+45°)) )
                         [ (Lon1-Lon0) ] 
 

Loxodrome Course

In the Mercator projection, the loxodrome is a straight line. The angle of intersection of the rhumb line with a vertical line is the true course C of the rhumb line and is given by:

  
  C = atan2( [X1-X0] , [Y1-Y0] )   

 
  C = atan2( [Lon1-Lon0] , 57.2958 * ln(tan(Lat1/2+45°)/tan(Lat0/2+45°)) )
 

(1)  
 

Loxodrome Distance

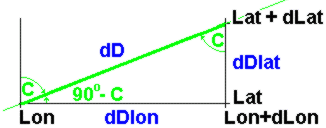
Also the distance along a loxodrome can be determined analytically. However, distances cannot be taken from the Mercator grid representation. This is because the "scale" of a Mercator chart depends on the Latitude, which is the "trick" to obtain parallel meridians in Mercator charts.

On the globe, with a Latitude-Longitude grid, there is a latitude dependent ratio between North-South and East-West distances. For a given Latitude Lat, the distances corresponding to 1°-of-Latitude and 1°-of-Longitude have a ratio of cos(Lat):

  distance_of_one_degree_EastWest = cos(Lat) * distance_of_one_degree_NorthSouth
 

To determine the distance along a loxodrome, consider an infinitesimal part of the loxodrome (on the globe) at some point L (Lat,Lon) between L0 and L1. The course C of the loxodrome is determined as described above.
The infinitesimal loxodrome path dD at a given latitude Lat has a longitude component dLon with length dDlon and a latitude component dLat with length dDlat. The length of this infinitesimal part of the loxodrome is given by:

  dD = sqrt( dDlon*dDlon + dDlat*dDlat )

(2)  

These infinitesimal distance components dDlon and dDlat correspond to a small change of Longitude (dLon) and Latitude (dLat) respectively:

  dDlon = dLon * cos(Lat) 
  dDlat = dLat

(3)  
(4)  

The distance components dDlon and dDlat are related to each other by the course angle:

  tan(C) = dDlon / dDlat
  dDlon  = tan(C) * dDlat

     
(5)  

Eliminating dDlon from (2) using (5) and expressing the result in change of Latitude yields:

  dD = dDlat * sqrt(tan2(C) + 1)  
     = dDlat / cos(C)    
     = dLat / cos(C)

  
  
(6)  

This identity has to be integrated beween Lat0 and Lat1 to obtain the total distance D of the loxodrome (notice that cos(C) is a constant for a loxodrome):

D =     dD = Lat1 Lat0 dLat     D = | Lat1 - Lat0 | cos(C)

(7)

The above equation is undefined for C=90° or C=270°. This is the case if L0 and L1 have the same Latitude (Lat0=Lat1) and equation (7) yields D = 0/0, which is undefined.

Instead being resolved for Latitude, the equations (2)-(5) may also be resolved for Longitude. Eliminating dDlat from (2) using (5) and expressing the result in change of Longitude yields:

  dD = dDlon / sin(C) = dLon * cos(Lat) / sin(C)

For a constant latitude (since C=90° / 270° ) this equation can be integrated between the Lon0 and Lon1:

D =     dD = cos(Lat) sin(C) Lon1 Lon0 dLon with | sin(C) | = 1.0     D = | cos(Lat0) * (Lon1 - Lon0) |

(8)

Notice that distances are always positive, so only the absolute value of D matters.

Summarizing, the loxodrome distance may be calculated by the following scheme (C is obtained from (1) as described above):

  D =  | 1/cos(C)  * (Lat1 - Lat0) |       if      Lat0 != Lat1

  D =  | cos(Lat0) * (Lon1 - Lon0) |       if      Lat0 == Lat1
 

Loxodrome Destination or the "Dead-Reckoning Problem"

The dead-reckoning problem is formulated as finding the current (estimated) position L1 (Lat1, Lon1), given a distance D sailed at a constant course C from a known location L0 (Lat0, Lon0).

The latitude difference between L0 and L1 can be easily obtained from (7):

  Lat1 = Lat0 + D * cos(C) 

(9)  

From the basic Equations (3), (4) and (5), describing how dDlon, dDlat, dLat and dLon are related, the following can be derived:

  dLon = tan(C) * dLat / cos(Lat) 

(10)  

Integrating both sides of the above differential equation yields:

Lon1 Lon0

dLon

=   tan(C) *

Lat1 Lat0

dLat cos(Lat)

this can be elaborated using the following equation:

dx cos(x)

= ln( tan(x/2 + 45°) )

For the change in Longitude and the corresponding change in Latitude, this yields:

  Lon1 - Lon0 = tan(C) * 57.2958 * ( ln(tan(Lat1/2 + 45°)) - ln(tan(Lat0/2 + 45°)) )  or

  Lon1 = Lon0 + tan(C) * 57.2958 * ln (tan(Lat1/2 + 45°) / tan(Lat0/2 + 45°) )

(11)  

Again, the scaling factor 57.2958 (180°/PI) assures the conformality while using angles expressed in degrees instead of radians. The value for "Lat1" is derived from equation (9).


Summarizing, first Lat1 is calculated from (9) and then Lon1 can be obtained from (11):

  Lat1 = Lat0 + D * cos(C)

  Lon1 = Lon0 + tan(C) * 57.2958 * ln (tan(Lat1/2 + 45°)/tan(Lat0/2 + 45°) )     if Lat1 != Lat0
       = Lon0 + D * cos(Lat0) * sin(C)                                           if Lat1 == Lat0
 

This solution is conform to solving the values of Lat1 and Lon1 from the identities (1), (7) and (8).