Anchoring Techniques
Deploying the primary anchor
Drop the anchor with the boat stationary or starting to drift back with the wind or tide.
Try to let the rode out consistently - avoid piling the chain up on top of the anchor.
A 5:1 ratio of rode-length to water-depth is minimum ("1" being the vertical distance from
the seabed to the bow roller - not the waterline). Generally speaking about 7:1 is appropriate.
Even if you plan on using short scope (e.g. if the anchorage is crowded), set the anchor at 5:1 first.
In any wind you can just let the bow wipe off. In calm conditions motor backward slowly.
Be careful, especially if using a new generation anchor - they can dig in so quickly that
any speed can damage equipment or crew.
In bad conditions, the ratio should be increased to 9:1, or even higher using maximum scope.
The rode's catenary effect on holding power is determined by the amount of chain and/or rope suspended
between the boat and the seabed, so the need for a high ratio decreases with increasing depth.
5:1 should remain the minimum. In very shallow water you need more than normal.
Then again, if your boat is in shallow water, it is probably well sheltered.
There are many variables and common sense should dictate.
After picking up the preferred spot, the predicted swinging area should be explored for waterdepht and
possible underwater obstructions. Then the boat is headed into the wind (or current, whichever is stronger).
Lower the anchor and take care not to pile up the chain on top of the grounded anchor as this will
prevent the anchor from setting correctly. Once the anchor is down, the rode is slowly veered up as the
boat drifts back. With little wind or current the motor will support the drifting backwards.
The anchor rode is secured with a chain snubber while reaching the desired scope.
After securing the anchor rode on deck (the anchor winch is not designed for snubbung anchor loads),
slowly increase the reverse powerd engine to 1500 RPM.
A transit marker abeam on the shore, should be checked to find out whether the anchor is dragging or not.
Also sensing the vibrations on the anchor chain at the bow with hand or foot, will indicate whether the anchor is dragging, bumping
over rock or sliding over mud.
If the anchor seems to sit well, turn off the engine, and let the boat settle in the pervailing wind or current.
The abeam onshore markers may be checked once again about 10 minutes later, to verify the boat has not moved slowly in that time.
If the anchor is not holding, the manoeuvre has to be redone maybe selecting a slightly different part
of the anchorage and maybe also using a better suited anchor type.
Some boats will "sail" at anchor, which means they will continually ride up on the rode then
fall back, or career from side to side. A high profile bow combined with a shallow underwater profile,
typical of modern sailing yachts, will exacerbate this.
The solution is to move the center of wind resistance farther aft, and this can be accomplished
with the use of a riding sail. These are available designed for both sail and power boats.
You should display appropriate signals while at anchor, in order to let other mariners identify
whether you are underway, drifting, or anchored. At night an all-round white light is required,
and during the day, a spherical "anchor-ball" suspended from the rigging (to create a circular silhouette).
Both should be sized according to the regulations for your vessel.
Anchoring under shifting Current and Wind Conditions
Bahamian moor
Bahamian moor, is an anchoring technique that is used in the Bahamian region with contrary wind and tidal currents.
One anchor is placed "upsteam" and one "downstream" and the vessel rides between the two with both anchor rodes
attached at the bow.
As the boat swings during current shifts, the first and second anchor alternate between the riding anchor under tention
(upstream) and the unloaded "lee" anchor (downstream) with the bow always pointing into the wind or current.
The Bahamian moor can also be used to limit the swing radius when anchoring elsewhere (e.g narrow creeks with limited
room to swing on one anchor).
Downsides of the Bahamian moor include the high risk of twisted rodes as result of a full curcle swing during current shifts
as well as the potential chafing if the slack anchor rode rubs on the vessel's hull or even snags on the keel,
possibly preventing the vessel from swinging freely. The latter can be prevented by - after setting the achors -
bridling the anchor rodes together at deck and then lowering both rodes until the bridle is well below the keel.
If one of the rodes is all chain, the weight of the chain is normally enough to accomplish this, but a kellet
may be needed if a combination of rope rodes is used.
Dual-Anchor mooring
Both anchors are set windward about 40 to 60 degrees apart, so the rodes form a "V" as seen from the bow.
The first (primary) anchor is set and settled upwind (or in the direction of the strongest expected wind)
with the required rode length, while memorizing the approximate position of the anchor.
Then the vessel must be motored upwind at a 45-degree angle up to a position abreast of the first anchor.
Here the second anchor is dropped.
If using rope, the location of the rode in the water must be carefully observed to avoid wrapping the
rope into the propeller.
After falling back between the two anchors, the length of both rodes may be adjusted as necessary.
The usage of marking buoys will simplify keeping track of the anchor positioning during the manoeuvre.
An added benefit of the dual-anchor mooring is the option to increase the length of the rode as the wind increases
and by doing so, reduce the angle between the two anchors to increase the holding power
(35 degrees is considered optimal in gale conditions).
To avoid twisting of the anchor ropes at the bow, a "Y" constellation may be used by shackling the secondary rode
to the all-chain primary one and lowering the chain until the bridle is well below the keel.
Heavy-Weather Anchoring
see also comments in document ...
Anchoring in heavy weather will put extreme stress on the ground tackle system.
Beyond a properly dimensioned anchor rode (storm anchor and rodes should be oversized),
chafe protection at all parts of the anchor rode
must be taken very serious to prevent a perilous weakening of the anchor system.
This includes using eye splices and thimbles for connecting rope to chain or shackles.
A proper eye splice should have a minimum of six full tugs and should be seized at each end
while the eye is under tention (to prevent the thimble from falling out of the eye under load).
For storm anchor rodes oval-shaped thimbles (without any sharp edged) should be used.
Also all shackle pins used in the system should be properly secured to prevent unexpected loosening.
Preparation and routine are the keys for secure anchoring.
Trying to deploy the anchor(s) in heavy weather is difficult (and sometimes impossible), so the
weather conditions should be observed and a safe anchorage should be reached with enough time to properly
deploy the planned anchor manoeuvre(s).
In riding out heavy wind, a vessel on a signle anchor rode will often sheer violently back and forth
across the wind. This tacking is often called "horsing" or "sailing at anchor" and will add a significant
additional dynamic load on the anchor rode.
Heavy-weater anchoring techniques must provide a way to reduce this "sailing at anchor"
and thus to reduce the peak-loading of the ground tackle system.
Hammerlock Moor
Heavy weather anchoring during conditions with high wind gusts cause the vessel to "horse" around
or jostle back-and-forth aggressively.
To counteract excessive horsing, the so called "Hammerlock Moor" anchoring technique may be used.
It consists of laying out a secondary anchor on a short scope, after the primary anchor is set.
The angle between the chains should be about 90 degrees, dropping the secondary achor at one extreme reach of a sheer.
The primary anchor takes most of the ground tackle load, allowing the secondary anchor to steady the bow and possibly
to drag along the bottom if the wind veers or backs.
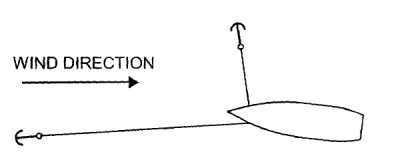In the hammerlock one anchor is deployed on short scope at a right angle to
the other anchor. This prevents the ship from sailing back and forth at the
anchor and reduces the dynamic loads experienced by the ship.
Properly executed, the hammerlock mooring will adjust itself to the shifting
wind of a hurricane or typhoon by allowing the short scope anchor to drag
as it comes under increasing load.
To accomplish this, the short scope anchor should be deployed on the side
toward the expected wind shift. In other words, if the wind is backing
(shifting counter-clockwise), the short scope anchor should be placed to
the port side of the ship. If the eye passes over the ship during the storm,
there will be a reversal of wind direction.
In this case, the short scope anchor of a hammerlock moor should be hauled
in until the anchor is just underfoot as the eye passes over.
In this way, the ship will be free to swing to the new wind direction without
twisting the anchor chains.
More chain can be veered out on the short scope anchor as the ship yaws to
its maximum point towards the wind shift to return to a hammerlock moor.
Clearly, this is an inherently risky operation in high winds, and all appropriate
precautions must be taken to minimize risk to the crew.
If the ship does begin to drag its long scope anchor, more chain may be
veered out to both anchors until the short scope anchor also holds solidly.
If the ship’s propulsion system is available it may be used to reduce the
load on the anchor.
Tandem-Anchor mooring
A tandem-anchor rig is a setup where two anchors are somehow connected in line with each other on a single rode.
It is a quick and easy way to increase the holding power of a single anchor rode.
The primary anchor is the one closest to the vessel and the tandem anchor is the one in front of the primary anchor.
The anchor rode consists of two sections, the primary rode and the tandem rode.
Preferebly, the tandem rode will be attached to a point near the attachment of the primary anchor such that
it is a mere extention of the primary rode.
The setup works best at dealing with strong winds from a single direction.
In general, this setup is recomended as superior alternative to a "V" or "Y" deployment, as the
two anchors work together more efficiently. In the tamdem configuration, the two anchors will be
contiuously under a shared load, whereas in the "V" or "Y" configuration the load tends to move from one anchor to the other,
more or less concentrated on just one, meaning that the overall capability of the system is determined by the weakest
of the two anchor rodes.
As a rule of the thumb, the length of the tandem rode may be the length of the boat. Only a few meters
is not enough, as enough slack is required to permit the primary anchor to set before the tandem.
Also, a greater length of the tamdem rode will allow the system to deal better with a veering pull direction.
Test have shown the use of tandem anchors increases the holding power by as much as 30 percent over
the holding power of the same two anchors deployed separately.
For even more holding power a combination of tandem ad dual mooring may be used.
This combines the increased holding power of the two anchors in line plus a third storm anchor
set in the opposite direction for even more security.
Modified Star mooring
Another excellent option for heavy weather anchoring is the modified star mooring combined with an oversized
kellet. The star mooring uses three separate anchors and rodes, each of which can be all chain, rope or a combination.
The anchors are deployed 120 degrees apart with the largest anchor set upwind (or in the direction of the strongest expected wind).
The rodes are shackled in the center between the anchor positions to a large mooring swivel, which in turn will be shackled
to a two-part bridle of two appropriatly sized stranded nylon lines, each having a galvanized thimble spliced at the bridle end.
The other ends of the nylon lines are properly secured on separate cleats on deck.
The holding power of this star configuration may be increased by adding an oversized kellet to the center of
the mooring system with the added benefit of reducing the vessel's swing radius and anchor sailing.
Recovering fouled anchors
...
Sources
|